电子罗盘(2):磁传感器误差源、硬磁干扰校准(3个参数)、实验验证
文章目录
- 理想情况
- 误差来源
-
- 内部
- 外部
- 误差模型
- 校准硬磁干扰(3个参数)
-
- 使用的模型
- 最小二乘法
- 实测结果
- 总结
- 代码和资料
-
- MATLAB代码
- 参考资料
- 样机
理想情况
在理想情况下,磁传感器的测量结果是完全准确的,三轴读数为三轴地磁场强度的投影: h = [ h x h y h z ] h x 2 h y 2 h z 2 = B 2 \textbf{h}=\left[ \begin{matrix} h_x\\ h_y \\ h_z \end{matrix} \right] \\ h_x^2 h_y^2 h_z^2 = B^2 h=??hxhyhz⎦⎤hx2+hy2+hz2=B2 因此,磁传感器在不同角度的测量值,落在一个球面 x 2 + y 2 + z 2 = B 2 x^2+y^2+z^2=B^2 x2+y2+z2=B2上,球心是原点,半径是B。
误差来源
主要分为磁传感器内部和外部因素造成的误差。
内部
主要是磁传感器灵敏度
-
三轴灵敏度不同,
例如,10uT的磁感应强度,分别用三个轴来测量,测量结果为:9uT,10uT,11uT。
-
三轴不正交
例如,某个磁场下,理想的读数是:[10uT,0,0],但实际上是[10uT,1uT,0],因为XY两轴不是完全正交,原来只在X轴有读数,在非理想情况下,Y轴上也有了一定读数。
-
零偏
在完全无磁场时也有一个非零读数。
几种误差对读数的影响示意图如下:(来自文末参考资料)
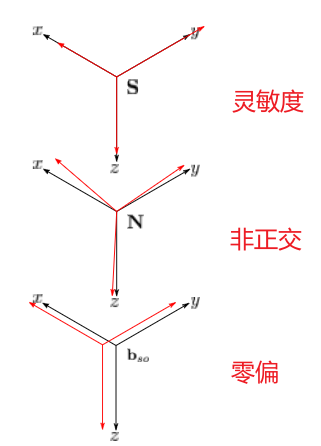
外部
-
硬磁干扰
硬磁干扰由传感器附近的永磁体等的磁场引起,造成的影响类似于零偏。
-
软磁干扰
软磁干扰是传感器附近的铁磁材料改变了原磁场的强度和方向。
详见磁传感器PCB设计指导 Layout Recommendations for PCBs Using a Magnetometer Sensor (nxp.com.cn)
误差模型
假设理想的测量结果为: h 0 = [ h 0 x h 0 y h 0 z ] \mathbf{h_0}=\left[ \begin{matrix} h_{0x}\\ h_{0y} \\ h_{0z} \end{matrix} \right] h0=⎣⎡h0xh0yh0z⎦⎤ 首先,外部的磁场由于软磁和硬磁干扰而发生了改变,先考虑外部的干扰: h m = I 3 × 3 h 0 + F h i \mathbf{h_m}=\mathbf{I_{3\times3}} \mathbf{h_0} + \mathbf{F_hi} hm=I3×3h0+Fhi I是3x3矩阵,用于表示软磁干扰, F s i \mathbf{F_si} Fsi为硬磁干扰造成的偏置。
考虑内部误差后,测量结果变为: h = S 3 × 3 N 3 × 3 h m + F o s = S 3 × 3 N 3 × 3 ( I 3 × 3 h 0 + F h i ) + F o s \mathbf{h} = \mathbf{S_{3\times3}} \mathbf{N_{3\times3}}\mathbf{h_m}+\mathbf{F_{os}}= \mathbf{S_{3\times3}} \mathbf{N_{3\times3}}(\mathbf{I_{3\times3}} \mathbf{h_0} + \mathbf{F_hi})+\mathbf{F_{os}} h=S3×3N3×3hm+Fos=S3×3N3×3(I3×3h0+Fhi)+Fos
其中,S、N为3x3矩阵,S表示三轴灵敏度差异,N表示三轴非正交的影响。 F o s \mathbf{F_{os}} Fos为3x1向量,表示零偏。
化简后,测量值h与实际值h0之间的关系可以表示为: h = W h 0 + V h 0 = W − 1 ( h − V ) \mathbf{h} = \mathbf{W} \mathbf{h_0} + \mathbf{V} \\ \mathbf{h_0} = \mathbf{W^{-1}}(\mathbf{h}-\mathbf{V} ) h=Wh0+Vh0=W−1(h−V) W是3x3矩阵,V是3x1向量。其中,W是一个对称矩阵(具体),因此只含6个系数。加上V的3个系数,总共需要获得9个系数才能实现校准。
但是,在某些场合只有硬磁干扰,而软磁干扰不明显,则此时 W = E \mathbf{W}=\mathbf{E} W=E, h = h 0 + V \mathbf{h} = \mathbf{h_0} + \mathbf{V} h=h0+V就只需要获得V的3个系数。
硬磁干扰的校准(3个参数)
使用的模型
如果只有硬磁干扰,则理论测量结果h0可表示为: h 0 = W − 1 ( h − V ) = h − V \mathbf{h_0} = \mathbf{W^{-1}}(\mathbf{h}-\mathbf{V} )=\mathbf{h}-\mathbf{V} h0=W−1(h−V)=h−V 理论测量结果落在球面上: h 0 T h 0 = ( h − V ) T ( h − V ) = B 2 \mathbf{h_0^T}\mathbf{h_0} = (\mathbf{h}-\mathbf{V})^T(\mathbf{h}-\mathbf{V})=B^2 h0Th0=(h−V)T(h−V)=B2 其中, h = [ h x h y h z ] , V = [ V x V y V z ] \textbf{h}=\left[ \begin{matrix} h_x\\ h_y \\ h_z \end{matrix} \right], \textbf{V}=\left[ \begin{matrix} V_x\\ V_y \\ V_z \end{matrix} \right] h=⎣⎡hxhyhz⎦⎤,V=⎣⎡VxVyVz⎦⎤ 展开后: h x 2 + h y 2 + h z 2 − 2 V x h x − 2 V y h y − 2 V y h y + V x 2 + V y 2 + V z 2 − B 2 = 0 h_x^2+h_y^2+h_z^2- 2V_xh_x- 2V_yh_y- 2V_yh_y + V_x^2 +V_y^2 +V_z^2 -B^2 = 0 hx2+hy2+hz2−2Vxhx−2Vyhy−2Vyhy+V 标签: 两轴磁传感器3p2261接近传感器