电磁感应、电感与变压器

??Biot-Savart定律指出电流元 I d l Idl Idl距离为 r r r任何P刺激的磁感应强度B的大小为 d B = k I d l sin θ r 2 dB = k{ {Idl\sin \theta } \over { {r^2} } } dB=kr2Idlsinθ

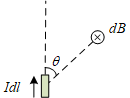
??图中 d B dB dB垂直于屏幕的方向。 k = μ 0 4 π k = { { {\mu _0} } \over {4\pi } } k=4πμ0​​， μ 0 \mu_0 μ0​是真空磁导率。磁感应强度B的方向满足右手螺旋定则。

  计算一根通电长直导线附近一点的磁感应强度B。长直导线是由无数个电流元组成，积分即可。

  在长直导线上建立坐标轴，与待求位置P水平的位置作为竖直方向的零点。直接积分，积分变量是 l l l，在有了坐标轴的情况下，我们就可以把这个曲线积分转化为定积分。

B = ∫ l d B = μ 0 I 4 π ∫ l sin ⁡ θ r 2 d l = μ 0 I 4 π ∫ − ∞ ∞ sin ⁡ θ r 2 d l B = \int\limits_l {dB} = { { {\mu _0}I} \over {4\pi } }\int\limits_l { { {\sin \theta } \over { {r^2} } }dl} = { { {\mu _0}I} \over {4\pi } }\int_{ - \infty }^\infty { { {\sin \theta } \over { {r^2} } }dl} B=l∫​dB=4πμ0​I​l∫​r2sinθ​dl=4πμ0​I​∫−∞∞​r2sinθ​dl

  但这还是不好求。可以想办法把 θ \theta θ作为积分变量，因为 θ \theta θ是在 ( 0 , π ) (0,\pi) (0,π)之间变化的。我们需要找到 d l dl dl与 d θ d\theta dθ的关系，还有 r r r和 θ \theta θ的关系。    r r r和 θ \theta θ的关系比较好找： r = a / cos ⁡ φ = a / cos ⁡ ( π − θ ) = − a / cos ⁡ θ r = a/\cos \varphi = a/\cos (\pi - \theta ) = - a/\cos \theta r=a/cosφ=a/cos(π−θ)=−a/cosθ    l l l与 θ \theta θ的关系是这样的： l = a tan ⁡ φ = a tan ⁡ ( π − θ ) = − a tan ⁡ θ l = a\tan \varphi = a\tan (\pi - \theta ) = - a\tan \theta l=atanφ=atan(π−θ)=−atanθ   两边微分后可得： d l = − a d θ / cos ⁡ 2 ( θ ) dl = - ad\theta/{\cos ^2}(\theta ) dl=−adθ/cos2(θ)   再把上面的结果代回到原来的积分式中

B = μ 0 I 4 π a ∫ 0 π sin ⁡ θ d θ = μ 0 I 2 π a B = { { {\mu _0}I} \over {4\pi a} }\int_0^\pi {\sin \theta d\theta = } { { {\mu _0}I} \over {2\pi a} } B=4πaμ0​I​∫0π​sinθdθ=2πaμ0​I​

  在分析问题的时候，除了通电长直导线附近磁场经常用到，还有环形电流轴线上的磁场也经常会遇到。

  环形电流上每一个电流元到轴线上一点的距离都相等，它们各自产生的磁感应强度叠加后， d B dB dB垂直于轴线方向的分量都抵消，只剩平行与轴线方向的分量。

B = ∫ l d B sin ⁡ θ = μ 0 I sin ⁡ θ 4 π r 2 ∫ l d l = μ 0 I sin ⁡ θ 4 π r 2 ⋅ 2 π R = μ 0 2 I R sin ⁡ θ r 2 B = \int\limits_l {dB} \sin \theta = { { {\mu _0}I\sin \theta } \over {4\pi {r^2} } }\int\limits_l {dl} = { { {\mu _0}I\sin \theta } \over {4\pi {r^2} } } \cdot 2\pi R = { { {\mu _0} } \over 2}{ {IR\sin \theta } \over { {r^2} } } B=l∫​dBsinθ=4πr2μ0​Isinθ​l∫​dl=4πr2μ0​Isinθ​⋅2πR=2μ0​​r2IRsinθ​   把 sin ⁡ θ = R r \sin \theta = {R \over r} sinθ=rR​， r = x 2 + R 2 r=\sqrt {x^2+R^2} r=x2+R2 ​代入得： B = μ 0 I R 2 2 ( x 2 + R 2 ) 3 / 2 B = { { {\mu _0}I{R^2} } \over {2{ {({x^2} + {R^2})}^{3/2} } } } B=2(x2+R2)3/2μ0​IR2​   当 x x x趋于无穷大时， x ≈ r x \approx r x≈r: B = μ 0 I S 2 π r 3 B=\frac{\mu_0IS}{2\pi r^3} B=2πr3μ0​IS​   S是圆环电流围成的面积。从这个公式中可以看出，圆环电流轴线上远处的某一点（ r r r确定）的 B B B的大小取决于 I I I和 S S S的乘积。因此定义了一个概念——磁偶极矩， p m p_m pm​。 p m = I S {p_m} = IS pm​=IS   磁偶极矩的方向和磁感应强度的方向相同，满足右手螺旋定则。