PLL锁相环基本原理介绍

在工作过程中，当输出信号的频率等于输入信号的频率时，输出电压与输入电压保持固定的相位差，即输出电压与输入电压的相位被锁定，这就是锁相环名称的由来。 锁相环是一个相位误差控制系统，通过比较参考信号和输出信号之间的相位误差来调整输出信号，以达到与参考信号相同频率的目的。其基本系统结构如下图1所示。 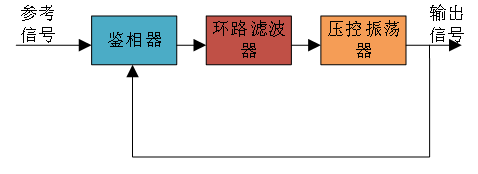图1 锁相环系统框图

基本锁相环由以下三部分组成

识别器通过比较输入信号和压控振荡器输出信号的相位，输出一定的电压信号。输出的电压信号是该信号相位差的函数，具体原理在第三部分介绍。

压控振荡器由环路滤波器输出电压控制，压控振荡器的振荡频率接近输出信号的频率，直到其频率相同。VCO用于锁定相位的输出信号与输入信号的相位保持着特定的关系。

各种形式的鉴相器。目前常用的是正弦波鉴相器，可用乘法器实现。 假设输入信号为 U i ( t ) = U i sin ( ω i t θ i ( t ) ) {U_i}\left( t \right) = {U_i}\sin \left( { {\omega _i}t {\theta _i}\left( t \right)} \right) Ui(t)=Uisin(ωi​t+θi​(t))，压控振荡器的输出为 U o ( t ) = U o cos ⁡ ( ω o t + θ o ( t ) ) {U_o}\left( t \right) = {U_o}\cos \left( { {\omega _o}t + {\theta _o}\left( t \right)} \right) Uo​(t)=Uo​cos(ωo​t+θo​(t))。

一般情况下， ω i {\omega _i} ωi​和 ω o {\omega _o} ωo​是不相等的，为了便于比较两者之间的相位差，需要将两者统一为 ω o {\omega _o} ωo​以为参考。

则输入信号变换为: U i ( t ) = U i sin ⁡ ( ω i t + θ i ( t ) ) = U i sin ⁡ ( ω o t + ( ω i − ω o ) t + θ i ( t ) ) = U i sin ⁡ ( ω o t + φ i ( t ) ) {U_i}\left( t \right) = {U_i}\sin \left( { {\omega _i}t + {\theta _i}\left( t \right)} \right) = {U_i}\sin \left( { {\omega _o}t + ({\omega _i} - {\omega _o})t + {\theta _i}\left( t \right)} \right) = {U_i}\sin \left( { {\omega _o}t + {\varphi _i}\left( t \right)} \right) Ui​(t)=Ui​sin(ωi​t+θi​(t))=Ui​sin(ωo​t+(ωi​−ωo​)t+θi​(t))=Ui​sin(ωo​t+φi​(t))

上式中 φ i ( t ) = ( ω i − ω o ) t + θ i ( t ) = Δ ω t + + θ i ( t ) {\varphi _i}\left( t \right) = ({\omega _i} - {\omega _o})t + {\theta _i}\left( t \right) = \Delta \omega t + + {\theta _i}\left( t \right) φi​(t)=(ωi​−ωo​)t+θi​(t)=Δωt++θi​(t)， Δ ω {\Delta \omega} Δω表示输出信号角频率与VCO振荡器信号角频率的差，是属于固有的频率差。

为了计算方便，将相位 θ {\theta } θ统一用 φ {\varphi } φ表示，改写VCO输出信号为 U o ( t ) = U o cos ⁡ ( ω o t + θ o ( t ) ) = U o cos ⁡ ( ω o t + φ o ( t ) ) {U_o}\left( t \right) = {U_o}\cos \left( { {\omega _o}t + {\theta _o}\left( t \right)} \right){\rm{ = }}{U_o}\cos \left( { {\omega _o}t + {\varphi _o}\left( t \right)} \right) Uo​(t)=Uo​cos(ωo​t+θo​(t))=Uo​cos(ωo​t+φo​(t))。

重新整理输出信号和VCO输出信号为：

前面谈到的鉴相器本质上就是一个理想模拟乘法器，所以将输入信号和VCO输出信号相乘。

这里用到数学上的积化和差公式: sin ⁡ α cos ⁡ β = 1 2 [ sin ⁡ ( α + β ) + sin ⁡ ( α − β ) ] \sin \alpha \cos \beta = \frac{1}{2}\left[ {\sin \left( {\alpha + \beta } \right) + \sin \left( {\alpha - \beta } \right)} \right] sinαcosβ=21​[sin(α+β)+sin(α−β)] 式(3-1)中两式相乘： U i ( t ) ⋅ U o ( t ) ⋅ A m = 1 2 U i U o A m [ sin ⁡ ( 2 ω o t + φ i ( t ) + φ o ( t ) ) + sin ⁡ ( φ i ( t ) − φ o ( t ) ) ] {U_i}\left( t \right) \cdot {U_o}\left( t \right) \cdot {A_m} = \frac{1}{2}{U_i}{U_o}{A_m}\left[ {\sin \left( {2{\omega _o}t + {\varphi _i}\left( t \right) + {\varphi _o}\left( t \right)} \right) + \sin \left( { {\varphi _i}\left( t \right) - {\varphi _o}\left( t \right)} \right)} \right] Ui​(t)⋅Uo​(t)⋅Am​=21​Ui​Uo​Am​[sin(2ωo​t+φi​(t)+φo​(t))+sin(φi​(t)