两个传感器滤波器
一辆车做变速直线运动,车上有GPS定位仪和速度表。两个传感器的数据通过卡尔曼滤波器优化了汽车的位置。 如果观察到的数据是向量z=[z1 z2].T。 z1为GPS定位位置,z二是速度表的速度读数。z协方差矩阵R~N(0,R)。 车辆状态方程的噪声是wk~N(0,Q)。 系统状态矩阵A=[1]预测值为上一位,最优估计为预测值,加测值与预测值差乘以比例。 卡尔曼滤波计算公式如下
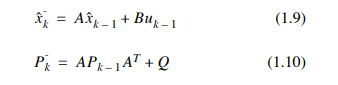
优化:提前计算Kk
关键要计算k,就是测量差的分配比例,通过(1.11) (1.10) (1.13)可以计算三种类型k,k只和系统噪声Q 与测量误差协方差矩阵R有关。因此,可以提前迭代几次k,然而,估计大量数据的计算位置。只需计算(1.9)式和(1.12)式。k提前计算。将卡尔曼五步简化为两步,大大降低矩阵计算量。
Python实现
如果车辆直线位置的真正方程是100 *(1 - np.exp(-t/10)), 传感器z1的方差为2,速度表z2的方差为0.2, R=[[2 0] ,系统噪声方差Q=[1]。 系统状态A=[1],观察矩阵H=[1 1].T [0 0.2]]
函数pre_kalman,通过参数A H Q R ,卡尔曼滤波参数可以提前计算K_K。迭代几次收敛。 函数obv()按方程100 *(1 - np.exp(-t/10)生成汽车的真实位置,加入高斯分布噪声,返回传感器观察 的数据z。z0为GPS位置数据,z一是速度。需要正确z1获得积分的位置。然后根据z和k_k估计卡尔曼滤波器。
一般GPS干扰位置方差大,速度表面差小,但积分后累积误差大。从图中可以看出,卡尔曼滤波器的估计值非常好。如图所示 附程序
import numpy as np import matplotlib import matplotlib.pyplot as plt from matplotlib.font_manager import FontProperties # 预设字体 font = {'family': 'SimHei', "size": 14} matplotlib.rc('font', **font) ''' 卡尔曼滤波,2路观察 ''' ''' 真实 x_k = A*xk_1 w_k w_k方差Q 观察 z_k = H*x_k v_k v_k方差R 预测 x_k_predict = A*x_k_est p_k_predict = A * p_k_est * A_T Q k_k = p_k_predict * H_T *( H*p_k_predict*H_T R)^-1 最优估计 x_k_est = x_k_predict k_k *( z_k - H*x_k_predict) p_k_est = (I - k_k * H) * p_k_predict ''' # 系统状态A A = np.mat([1]) # 两个观察仪器观察矩阵 H = np.mat([[1], [1]]) #观察仪器方差sigma1 sigma2 sigma1 = 2 sigma2 = 0.2 #系统噪声wk方差Q Q = np.mat(1) '''由Q R算kk''' def pre_kalman(A,H): R=np.mat([[sigma1, 0],[0, sigma2]]) I=np.mat([1]) p_est = np.mat([0]) #估计协方差矩阵 for _ in np.arange(0,10,1): p_predict = A * p_est * A.T Q #预测协方差矩阵 kk = p_predict * H.T * (H * p_predict * H.T R).I p_est = (I - kk * H) * p_predict return kk #返回k_k ''' 两个测量仪器测量两组信号,z位置测量值为0,z1.速度测量值 z0的方差为sigma1,z1方差为sigma2 真实信号为1-exp(t/10) ''' def obv(): t = np.linspace(1,100,100) real = 100 *(1 - np.exp(-t/10)) #real = t**2 #求速度xdot dt = t[1:] - t[:-1] dx = real[1:] - real[:-1] xdot = dx / dt #补第0个对齐 xdot = np.hstack([real[0],xdot]) #真实信号真实噪声,模拟测量仪器的误差噪声 t = t[:-1] real=real[:-1] xdot=xdot[:-1] z1= real np.random.normal(0,sigma1,size=t.shape[0]) z2= xdot np.random.normal(0,sigma2,size=t.shape[0]) z = np.mat([(a,b) for (a,b) in zip(z1,z2)]) return [t, dt, real,z] ''' 计算卡尔曼 z是观察到的数据 kk是卡尔的慢比例系数 ''' def calc_kalman(A,H,z_k,kk): global x_est x_pred = A * x_est x_est = x_pred kk * (z_k - H * x_pred) return x_est global x_est #最佳估计值 if __name__ == '__main__': #算k值 kk = pre_kalman(A,H) #生成观察仪器信息Z,返回时间,真实值,两个观察仪器的噪声值 [t, dt, xreal, z] = obv() x_est=np.mat([0]) x_est_list=[] z1_integral=0 for k in range(z.shape[0]): #积分速度 z1_integral = z[k][0,1] * dt[k] z[k][0,1] = z1_integral #计算卡尔曼,结果是x_est calc_kalman(A, H, z[k].T, kk) x_est_list.append(x_est[0,0]) x_est_list=np.array(x_est_list) plt.title(卡尔曼滤波器) plt.plot(t, xreal, label='真实',color='g') plt.plot(t, z[:,0], label='位置测量',color='b') plt.plot(t, z[:,1], label=速度积分,color='y') plt.plot(t, x_est_list, label='估计',color='r') plt.legend(loc="lower right") plt.show()