• 图结构是一种与树结构有些相似的数据结构

• 图论是数学的一个分支，而且在数学中，树是图的一种

• 图论以图为研究对象，研究顶点和边组成的图形的数学理论和方法

• 主要研究目的如下：事物之间的联系系，顶点代表事物，边代表两件事之间的关系

• 一组顶点：通常用V（Vertex）表示顶点的集合

• 一组边：通常用E（Edge）表示边的集合

  • 边缘是顶点和顶点之间的连线

  • 边可以是有向是的，也可以无向的。比如 A—B 表示无向， A—> B 表示有向

• 顶点：表示图中的一个节点；

• 边：表示顶点和顶点连间的连接；

• 相邻顶点：由一边连接在一起的顶点称为相邻顶点；

• 度：顶点度是相邻顶点的数量；

• 路径：

  • 简单路径：路径要求简单不包含重复的顶点；

  • 回路：第一个顶点与最后一个顶点相同路径称为回路；

• 无向图：图中的一切没有方向的；

• 向图：图中的一切边缘有方向的；

• 无权图：无权图中的边没有权重意义；

• 带权图：带权图中的边具有一定的权重意义；

表示图的常用方法是：邻接矩阵。

• 可以使用二维数组表示邻接矩阵；

• 邻接矩阵让每个节点和整数相关联，该整数作为数组的下标值；

• 使用一个二维数组来表示顶点之间的连接；


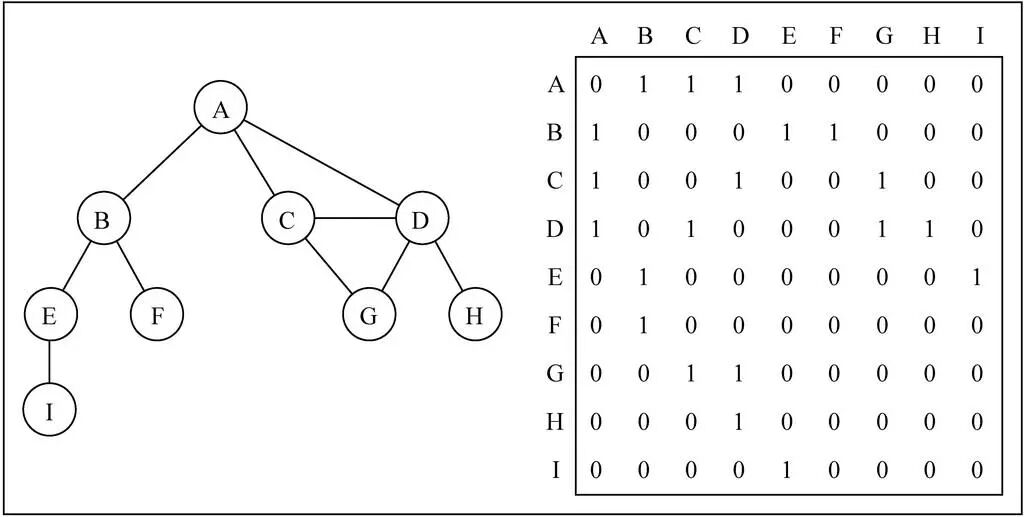
如上图所示：

• 二维数组0表示没有连线，1表示有连线；

• 如：A[ 0 ] [ 3 ] = 1，表示 A 和 C 之间有连接；

• 邻接矩阵的对角线上的值为0，表示A - A ，B - B，等自回路都没有连接(与自己没有联系)；

• 若为无向图，则对角线上所有元素的对称矩阵应为0；

若图为一稀疏图，然后邻接矩阵中将存在大量的 0，造成**浪费存储空间 **

另一种常用的表示图方式是：邻接表。

• 图中有邻接表与顶点相邻的每个顶点和顶点列表组成；

• 这个列表是可用的存储方式多种多样，比如：**数组/链表/字典（哈希表）**等都可以；

![AMMKaTeX parse error: Expected 'EOF', got '}' at position 1: }?5Y5H(`J5JP4EHG}…}5Y5H(`J5JP4EHG}V]Y.jpg&originHeight=632&originWidth=1024&originalType=binary&ratio=1&rotation=0&showTitle=false&size=40721&status=done&style=none&taskId=u300123d3-932d-408e-a18d-c81e420def0&title=&width=540)

如上图所示：

• 图中可清晰看到A与B、C、D相邻，如果要表示这些与A顶点相邻的顶点(边)，可以通过它们作为A值（value）存储在相应的数组/链表/字典中。

• 之后，通过键（key）A取出相应的数据非常方便；

• 邻接表可以简单得到出度，也就是说，一个顶点指向其他顶点的数量；

• 但是，计算邻接表入度(指向某一顶点的其他顶点的数量称为该顶点的入度)非常困难。此时需要结构逆邻接表有效计算入度；

在实现过程中使用邻接表表示边的方式，使用字典类存储邻接表

首先，需要引入以前实现的字典和队列

///包装字典 function Dictionary() { 
         //字典属性 this.items = { 
         } //字典操作方法 //一.在字典中添加键值对 Dictionary.prototype.set = function (key, value) { 
          this.items[key] = value } //二.判断字典中是否有某个key Dictionary.prototype.has = function (key) { 
          return this.items.hasOwnProperty(key) } //三.从字典中移除元素 Dictionary.prototype.remove = function (key) { 
          //1.判断字典中是否有这个key if (!this.has(key)) return false //2.从字典中删除key delete this.items[key] return true } //四.根据key获取value Dictionary.prototype.get = function (key) { 
          return this.has(key) ? this.items[key] : undefined } //五.获取所有keys Dictionary.prototype.keys = function () { 
          return Object.keys(this.items) } //六.size方法 Dictionary.prototype.keys = function () { 
          return this.keys().length } //七.clear方法 Dictionary.prototype.clear = function () { 
          this.items = { 
         } } } //封装队列类 function Queue() { 
          //属性 this.items = [] //方法 //1.enqueue Queue.prototype.enqueue = (element) => { 
          this.items.push(element) } //2.dequeue Queue.prototype.dequeue = () => { 
          return this.items.shift() } //3.front Queue.prototype.front = () => { 
          return this.items[0] } //4.isEmpty Queue.prototype.isEmpty = () => { 
          return this.items.length === 0 } //5.size Queue.prototype.size = () => { 
          return this.items.length } //6.toString Queue.prototype.toString = () => { 
          return this.items.join('') } } 

function Graph (){ 
        
  //属性：顶点（数组）/边（字典）
  this.vertexes = []//顶点
  this.edges = new Dictionary()//边
}

创建一个数组对象vertexes存储图的顶点；创建一个字典对象edges存储图的边，其中key为顶点，value为存储key顶点相邻顶点的数组。 代码实现：

Graph.prototype.addVertex = function (v) { 
        
  this.vertexes.push(v)
  this.edges.set(v, [])
}
Graph.prototype.addEdge = (v1,v2){ 
        
  this.edges.get(v1).push(v2)
  this.edges.get(v2).push(v1)
}

测试代码：

let graph = new Graph()
let myVertexes = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']
for (let i = 0; i < myVertexes.length; i++) { 
        
  graph.addVertex(myVertexes[i])
}
graph.addEdge('A', 'B');
graph.addEdge('A', 'C');
graph.addEdge('A', 'D');
graph.addEdge('C', 'D');
graph.addEdge('C', 'G');
graph.addEdge('D', 'G');
graph.addEdge('D', 'H');
graph.addEdge('B', 'E');
graph.addEdge('B', 'F');
graph.addEdge('E', 'I');
console.log(graph)

测试结果：



为图类Graph添加toString方法，实现以邻接表的形式输出图中各顶点。

代码实现：

Graph.prototype.toString = () => { 
        
  let resultString = ''
  for (let i = 0; i < this.vertexes.length; i++) { 
        
    resultString += this.vertexes[i] + ' ---> '
    let vEdge = this.edges.get(this.vertexes[i])
    for (let j = 0; j < vEdge.length; j++) { 
        
      resultString += vEdge[j] + ' '
    }
    resultString += '\n'
  }
  return resultString
}

测试代码：

console.log(graph.toString())

测试结果：


• 图的遍历思想：

  • 图的遍历思想与树的遍历思想一样，意味着需要将图中所有的顶点都访问一遍，并且不能有重复的访问

• 遍历图的两种算法

  • 广度优先搜索（Breach - First Serch，BFS）

• 深度优先搜索（Depth - First Serch ，DFS）

• 两种遍历算法都需要指定第一个被访问的的顶点

• 为了记录顶点是否被访问过，使用三种颜色来表示他们的状态

  • 白色：表示该顶点还没有被访问过

  • 灰色：表示该顶点被访问过，但其相邻顶点并未完全被访问过

  • 黑色：表示该顶点被访问过，且其相邻顶点都被访问过

首先封装initializeColor方法，将图中所有顶点初始化为白色，代码实现如下

Graph.prototype.initializeColor = () => { 
        
  let colors = []
  for (let i = 0; i < this.vertexes.length; i++) { 
        
    colors[this.vertexes[i]] = 'white'
  }
  return colors
}

• 广度优先搜索算法会从指定的第一个顶点开始遍历图，先访问其所有的相邻顶点，就像一次访问图的一层

• 也可以说是先宽后深的遍历图中的各个顶点

![5MHP8)ZKaTeX parse error: Expected 'EOF', got '#' at position 99: …39837afea8.jpeg#̲clientId=ua8b1b…GPW1IF`B0TG4XYW.jpg&originHeight=687&originWidth=1024&originalType=binary&ratio=1&rotation=0&showTitle=false&size=48469&status=done&style=none&taskId=u77ca0b46-99a1-4fe0-8144-db7da85ab44&title=)

实现思路：

基于队列可以简单地实现广度优先搜索算法：

• 首先创建一个队列Q（尾部进，首部出）；

• 调用封装的initializeColor方法将所有顶点初始化为白色；

• 指定第一个顶点A，将A标注为灰色（被访问过的节点），并将A放入队列Q中；

• 循环遍历队列中的元素，只要队列Q非空，就执行以下操作：

  • 先将灰色的A从Q的首部取出；

  • 取出A后，将A的所有未被访问过（白色）的相邻顶点依次从队列Q的尾部加入队列，并变为灰色。以此保证，灰色的相邻顶点不重复加入队列；

  • A的全部相邻节点加入Q后，A变为黑色，在下一次循环中被移除Q外；

代码实现：

Graph.prototype.bfs = (initV, handler) => { 
        
  let colors = this.initializeColor()
  let que = new Queue()
  que.enqueue(initV)
  while(!que.isEmpty()){ 
        
    let v = que.dequeue()
    let vNeighbours = this.edges.get(v)
    colors[v] = 'gray'
    for (let i = 0; i < vNeighbours.length; i++) { 
        
      const a = vNeighbours[i]
      if(colors[a] == 'white'){ 
        
        colors[a] = 'gray'
        que.enqueue(a)
      }
    }
    handler(v)
    colors[v] = 'black'
  }
}

测试代码：

//4.测试bfs遍历方法
let result = ""
graph.bfs(graph.vertexes[0], function(v){ 
        
  result += v + "-"
})
console.log(result);

测试结果:


• 深度优先搜索算法会从指定的第一个顶点开始遍历图，沿着路经直到这条路径的最后一个顶点被访问了

• 接着原路回退，并探索下一条路径


实现思路：

• 可以使用栈结构来实现深度优先搜索算法；

• 深度优先搜索算法的遍历顺序与二叉搜索树中的先序遍历较为相似，同样可以使用递归来实现（递归的本质就是函数栈的调用）。

• 基于递归实现深度优先搜索算法：定义dfs方法用于调用递归方法dfsVisit，定义dfsVisit方法用于递归访问图中的各个顶点。

• 在dfs方法中：

  • 首先，调用initializeColor方法将所有顶点初始化为白色；

  • 然后，调用dfsVisit方法遍历图的顶点；

• 在dfsVisit方法中：

  • 首先，将传入的指定节点**v标注为灰色；

**

• 接着，处理顶点V；

• 然后，访问V的相邻顶点；

• 最后，将顶点V标注为黑色；

代码实现：

Graph.prototype.bfs = (initV, handler) => { 
        
  let colors = this.initializeColor()
  let que = new Queue()
  que.enqueue(initV)
  while(!que.isEmpty()){ 
        
    let v = que.dequeue()
    let vNeighbours = this.edges.get(v)
    colors[v] = 'gray'
    for (let i = 0; i < vNeighbours.length; i++) { 
        
      const a = vNeighbours[i]
      if(colors[a] == 'white'){ 
        
        colors[a] = 'gray'
        que.enqueue(a)
      }
    }
    handler(v)
    colors[v] = 'black'
  }
}

测试代码：

//4.测试bfs遍历方法
let result = ""
graph.dfs(graph.vertexes[0], function(v){ 
        
  result += v + "-"
})
console.log(result);

测试结果: