matlab低通滤波器的设计
文章目录
-
- matlab低通滤波器的设计
- 前言
- 一、什么是滤波器？
- 二、二。滤波器的技术指标
- 三、滤波器分类
- 四、巴特沃斯低通滤波器设计
-
- 1.设置输入信号
- 2.设计滤波器
- 3.滤波器输出信号
- 五、采用ADI公司滤波器向导设计滤波器
前言
例如，随着人工智能的不断发展，机器学习技术变得越来越重要。许多人开始学习机器学习。本文介绍了机器学习的基本内容。
一、什么是滤波器？
顾名思义，滤波器是一种具有频率选择功能的电路和操作处理系统。 滤波器根据使用器件的不同分为。无源滤波器由无源设备的电阻、电容和电感组成，利用感应设备的阻抗特性随频率变化而变化。 无源滤波器的优点是结构简单，不需要电源，可靠性高。缺点是通频带内的信号能量会丢失，使用传感器件会引起电磁感应，大电感会影响滤波器的体积。 有源滤波器由无源设备和有源设备组成。通常，有源滤波器由集成运输、放电、电阻和电容组成，不需要电感。因此，电路体积小，重量轻。有源滤波器的优点是输出阻抗低，输入阻抗和开环增益高，多级连接时相互影响小，容易形成多级滤波器，滤波器体积小。缺点是有源设备需要电源，功耗可靠性不如无源滤波器，不适用于某些高压大功率场合。
二、二。滤波器的技术指标
滤波器特性可以用其频率响应来描述，按其特性的不同，可以分为低通滤波器，高通滤波器，带通滤波器和带阻滤波器等。滤波器的阶数，滤波器的阶数是指在滤波器的传递函数中有几个极点，阶数同时也决定了转折区的下降速度，一般每增加一阶(一个极点)。 决定滤波器阶数的技术指标主要包括：（
三、滤波器分类
滤波器可根据频率响应分为巴特沃斯（Butterworth）过滤器，贝塞 尔（Bassel）滤波器，切比雪夫（Chebyshev）滤波器，椭圆（Eliptic）滤波器等种 类。这四种滤波器的特滤波器的特：
| 滤波器种类 | 特性 |
|---|---|
| 巴特沃斯滤波器 | 通带和阻带没有起伏，通带范围内的特征曲线是 |
| 贝塞尔滤波器 | 阻带内的衰减小于巴特沃斯，截止特性差，具有 |
| 与雪夫滤波器相比 | 具有，在通带内等波纹起伏 |
| 椭圆滤波器 | 过渡带衰减特性最陡， |
四、巴特沃斯低通滤波器设计
1.输入信号设置
代码如下(示例):
%% Parameter InterfaceFrequence = 60; %单位：Hz Frequence1 = 1e3; %单位：HzFrequence2 = 1.8e3; %单位：HzSampleFre = 4e3; %单位：HzSampleLen = SampleFre; %采样点数%% Main%-------------------产生三路信号t = 0:1/SampleLen:1/SampleFre*(SampleLen-1);SignalData0 = sin(2*pi*Frequence0*t);SignalData1 = 2*sin(2*pi*Frequence1*t);SignalData2 = 3*sin(2*pi*Frequence2*t);SignalData3 = SignalData0+SignalData1+SignalData2;figure;hold onplot(t(1:150),SignalData0(1:150),'b')plot(t(1:150),SignalData1(1:150),'r')plot(t(1:150),SignalData2(1:150),'k')title('输入信号成分')hold offfigure;plot(t(1:150),SignalData3(1:150))title('三路信号求和')%-------------------输入信号频域图FFT_Data = abs(fft(SignalData3));m = FFT_Data(1:length(FFT_Data)/2);n = length(SignalData3);f = (1:n/2)*(SampleFre/n);figure;plot(f,m)xlabel('Frequency')ylabel('Power')title('输入信号频谱')输入信号为：sin(2pi60t)+2sin(2pi1000t)+sin(2pi18000t) 输入信号的时域图：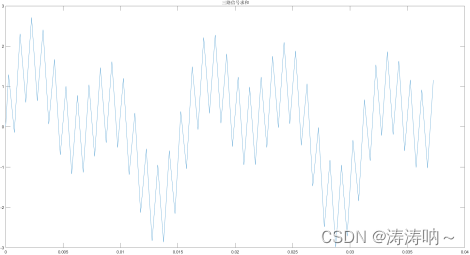 
输入信号的频域图：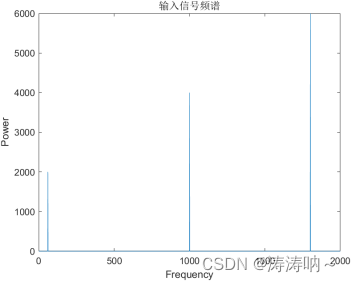 
输入信号采样频率为4000Hz。
2.设计滤波器
利用命令filterDesigner启动matlab滤波器设计模块，如下图所示：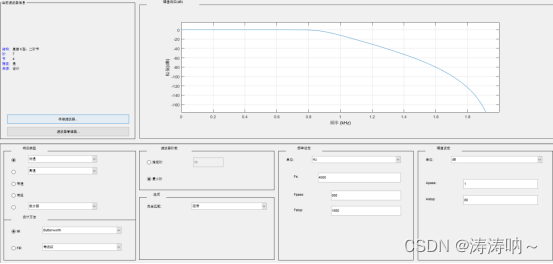 
滤波器的类型为低通巴特沃斯滤波器，滤波器阶数选择为最小阶数； （ 滤波器的如下图所示： 
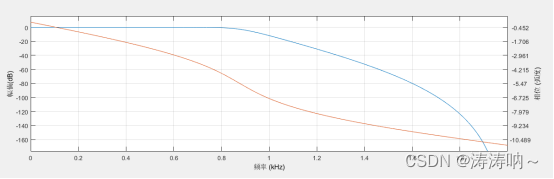matlab自带的滤波器设计工具，可以将该设计好的滤波器变量导出至工作区 
工作区就会出现一个Hd的对象，再用filter函数对输入信号进行滤波，代码如下：
%% 滤波器设计 filterDesigner %% 信号滤波后 y = filter(Hd,SignalData3); figure;plot(t(1:150),y(1:150));title('输出信号时域') y_Data = abs(fft(y));m = y_Data(1:length(y_Data)/2);n = length(y);f = (1:n/2)*(SampleFre/n);figure;plot(f,m);title('输出信号频谱')xlabel('Frequency')ylabel('Power')matlab设计的滤波器可以导出至simulink实现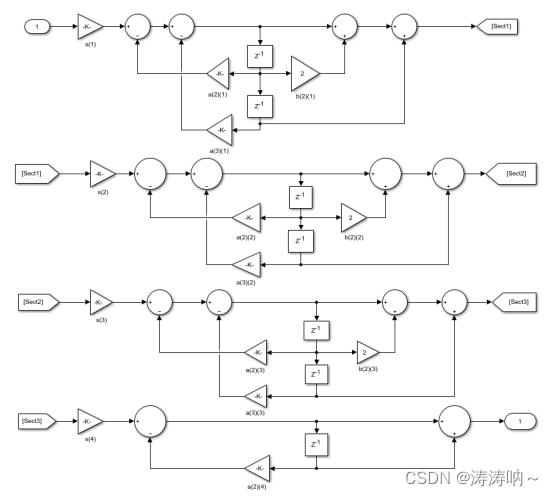 
3.滤波器输出信号
输入信号经过滤波器滤除掉了高于频率1.6KHz的信号分量。 所以输出信号时域图为：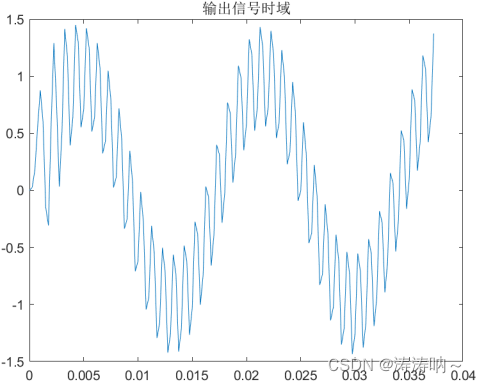 
输出信号的频域图为：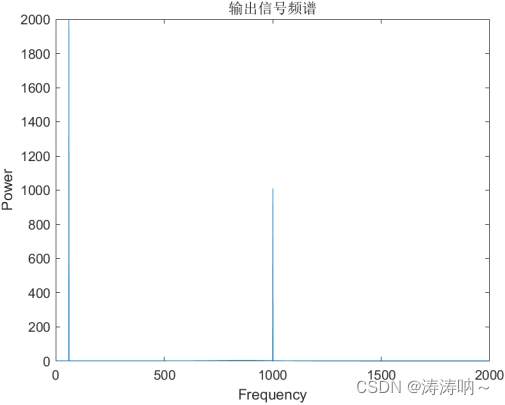 
五、采用ADI公司的滤波器向导设计滤波器
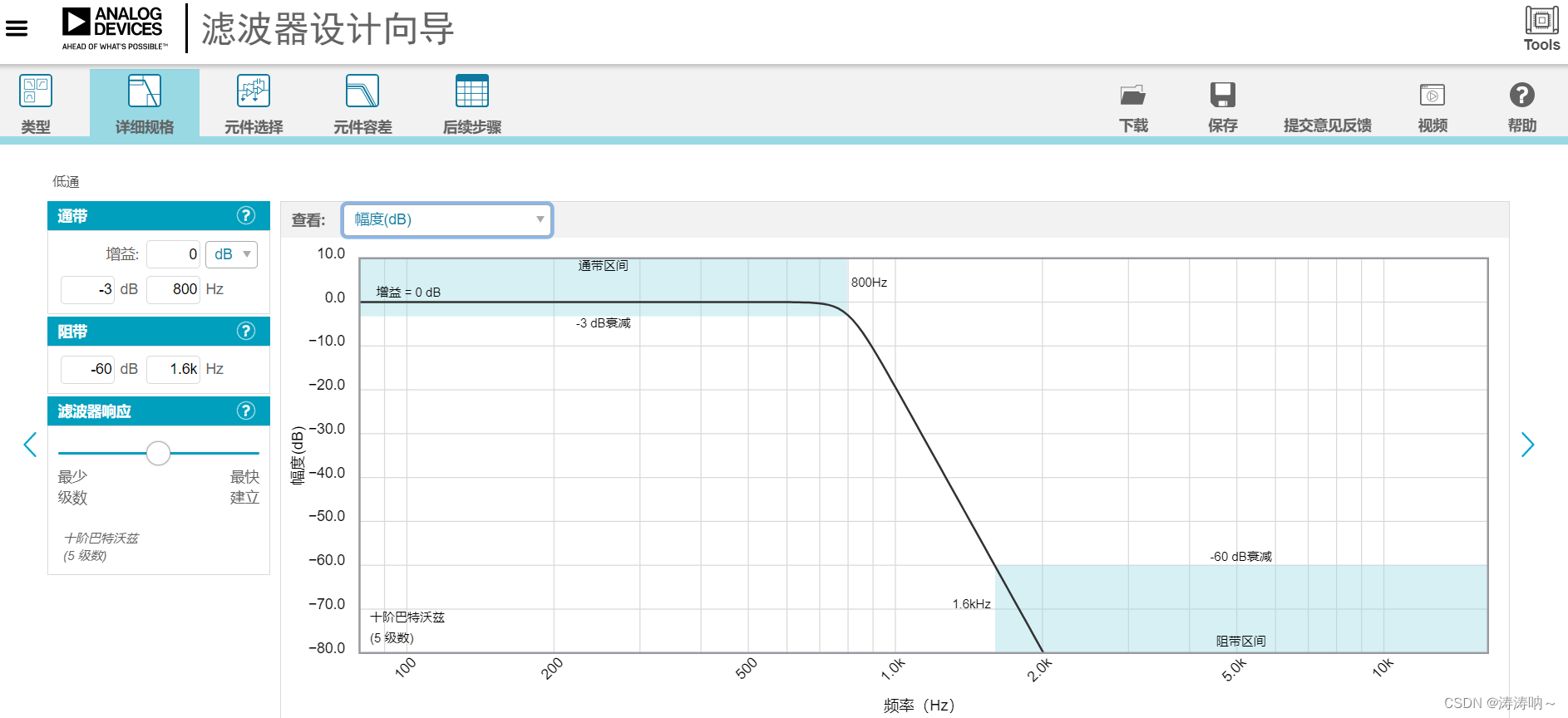ADI公司的滤波器向导还提供电路实现参考图： 