机器学习知识
Q 问题们
1.归一化层加在哪里?它不同于数据预处理中的归一化?dropout加在哪里,什么时候用?
答:全连接层一般加入归一化层FC和卷积层conv后面,激活层之前。dropout似乎一般都在FC防止过拟合。
以前在神经网络训练中,只对输入层数据进行归一化处理,。要知道,虽然我们对输入数据进行了归一化处理,但是输入数据了σ ( W X b ) 这样的矩阵乘法和非线性操作之后,其。如果能在网络中间进行归一化处理,是否能改善网络训练?答案是肯定的。
2.如何设置卷积核内容?通常看设置卷积核的大小,没有看到设置卷积核的内容?
答:卷积核是算法自己学习的,也就是说。卷积核的内容代表权重。高斯滤波器应该是什么?
3.卷积核滑动窗也有步长吗?这里的步长有什么用?same、valid有关系吗?也就是说,图像大小在完成卷积后是否会改变。
4.不同通道的卷积核值不同吗?比如这张图:
(对了,卷积核的通道数应与输入图像的通道数一致)
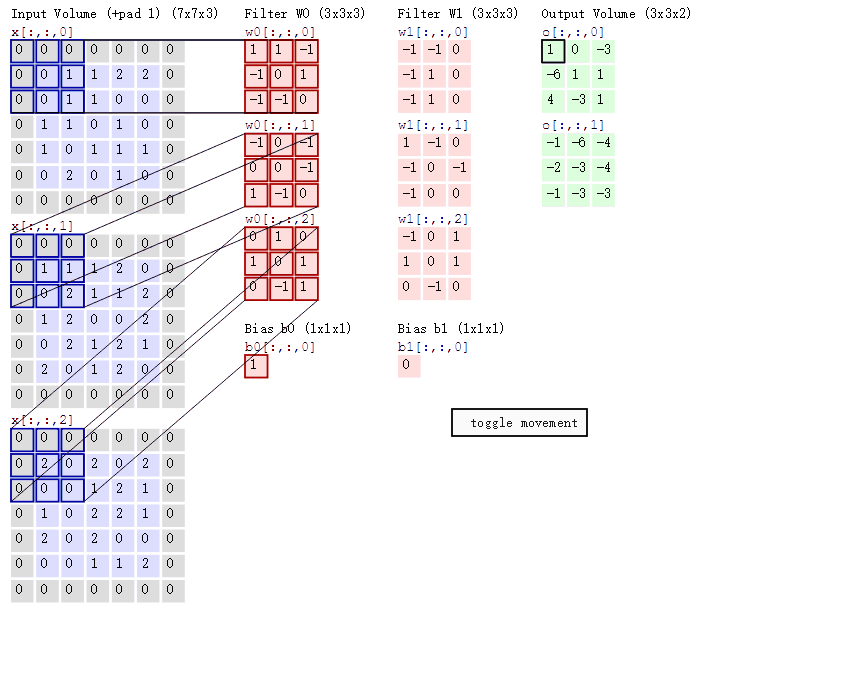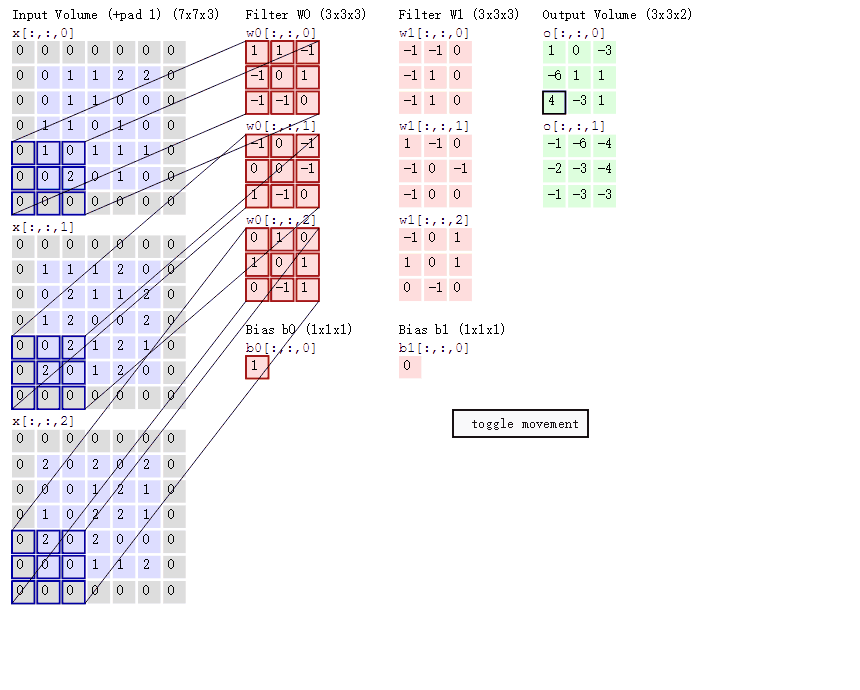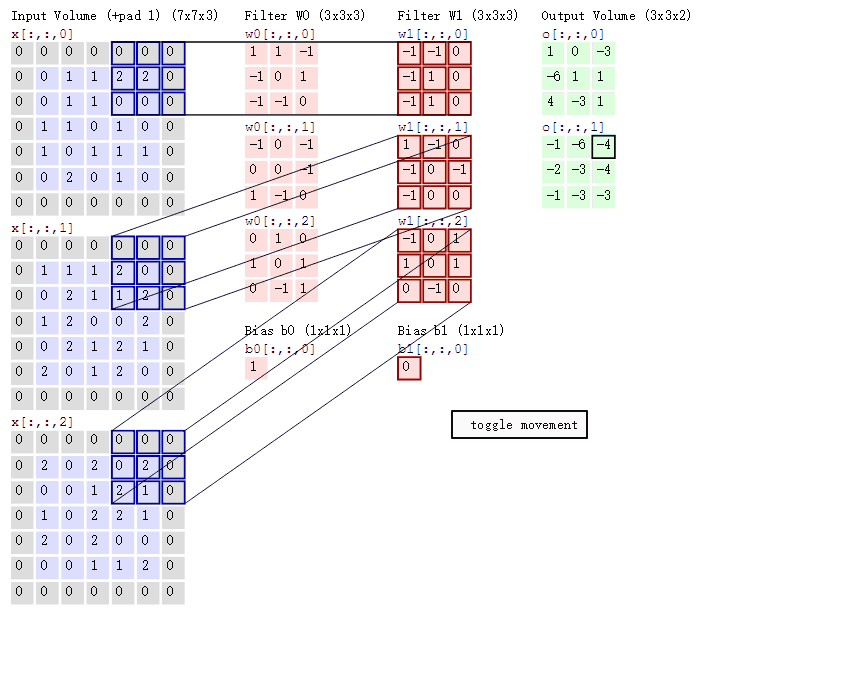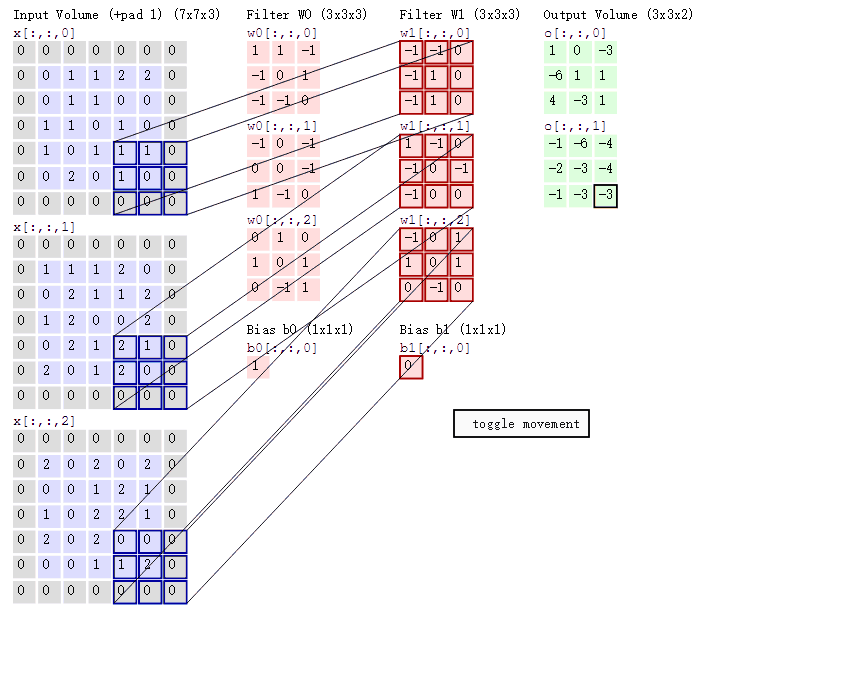
5.卷积层也有步长吗?设置在代码的地方?
6.1×1卷积核有什么用?
答:大型网络将应用于1,以减少参数×1卷积核。
0 一些不严谨的感觉
-
若特征过多,则采用归一化、标准化等处理。
-
学习sklearn这个库里有很多函数,直接调用fit可以拟合。
-
一般都是为了好的拟合而寻找方案是呈现成本函数,找到最低点很方便。
-
是主要类型。
-
有些公式中时,,这是为了,使。
-
决策边界是模型函数绘制的曲线。
-
采用上采样、下采样场景:(分类时)正负样本分布不平衡。
-
在代码中,在前面添加此行,以避免莫名其妙的红字显示。
import warnings warnings.filterwarnings('ignore') -
dense表示全连接层。
-
LRN:局部响应归一化。
-
变形卷积核,可分离卷积?卷积神经网络十大拍案惊艳。
-
在相同的网络下,pre-training fine-tuning work最好的。论文阅读笔记:Object Detection Networks on Convolutional Feature Maps
※ 积累
※.1 数据集
链接1 ??链接2
可到全国数字博物馆集群-博物中国去爬虫
※.2 数据增强模式
-
YOLOv5中的马赛克增强模式
-
生成高斯混合模型对抗网络数据增强算法
-
利用Albumentations数据增强工具。Pytorch使用albumentations实现数据增强
-
预处理
- 原始数据,然后将图像尺寸归一化,通过平移、翻转等数据操作扩展数据集
- 原始数据集的尺寸直接归一化,不同角度的数据增强翻转
-
Keras图像数据增强工具提供Image Data Generator
※.3 Github代码
1 一些基本概念
1.0 监督员的定义
参考博客:有监督、半监督、无监督、弱监督、自监督的定义和区别
简单比喻全监督、半监督、无监督学习
-
无监督:无标签数据培训;(平时做的题目没有答案;)
-
半监督:同时使用标签和无标签数据进行培训。最近很热,这个领域发展很快。以前通常是两个阶段的训练,先用标签数据训练(小规模)Teacher模型,然后用这个模型预测伪标签(大规模)无标签数据,作为Student模型训练数据;目前直接有很多end-to-end地面训练,大大减少半监督训练工作;(平时做的题目,一半有答案;)
-
自我监督:训练无标记数据,让模型通过一些方法学习数据inner representation,再接下游任务,比如加一个mlp作为分类器等。但在接受下游任务后,您仍然需要在特定的标签数据上finetune,只是有时候可以选择完全固定前层,只是finetune网络连接的网络参数。(域适应:在平时做的题目中,总结训练,将经验转移到高考中,做出答案。)
-
弱监督:用有标签数据训练。(平时做的题有答案,但答案不一定正确;)
上述概念的分类并不严格相互排斥。
1.1 性能评价指标
1.1.0 baseline,backbone和benchmark
一般用benchmark data 做实验,测试A B C D四个模型,然后结果假设是的模型C,作为baseline,看看其他模型比C增加了多少。
直接用别人的模型baseline,然后在别人的模型上添加各种模型components。那这个时候可以把baseline看成benchmark。我的理解是benchmark在不同的语境下,它是每个人都认可的标准benchmark指令可能不同。例如,有人得到了一个非常好的数据集,它对应于某个数据集task,那么作者肯定会提出解决方案task模型,然后很多人follow这个task,这个数据集自然是benchmark data,这种方法是benchmark method(model)。baseline和benchmark有什么区别?
-
(基线):模型能达到的;
-
:现在的模型能达到更好的效果;再往上就是state of art(SOTA)行业顶尖。
-
(核心、支柱):骨干网络。在神经网络中,尤其是CV一般先领域(常见的有vggnet,resnet,谷歌的inception),这部分是整个CV任务的基础,因为后续的下游任务是基于提取的图像特征(如分类、生成等)。backbone是什么意思
1.1.1 模型评价指标AUC(area under the curve)
AUC是机器学习领域的模型评价指标。根据维基百科的定义,AUC(area under the curve)是ROC曲线下的面积。
参考博客:模型评价指标:AUC(area under the curve)
评价指标要好好的去设计一下,因为正负样本可能不均衡。
1.1.2 二分类问题
正样本(positive)、负样本(negative)
:预测为真,实际为真
:预测为假,实际为假
:预测为假,实际为真。
:预测为真,实际为假。
(recall),也称(true positive rate,TPR),,。(实际正样本中被预测为正的概率,横着看) Recall ( T P R ) = T P T P + F N \operatorname{Recall}(T P R)=\frac{T P}{T P+F N} Recall(TPR)=TP+FNTP (precision)也称,,阳性预测值(positive predictive value, )。(预测为正样本中被预测为正的概率,竖着看) Precision ( P P V ) = T P T P + F P \operatorname{Precision}(PPV)=\frac{TP}{TP+FP} Precision(PPV)=TP+FPTP 也称 (F1-Score),描述的是召回率与精确度之间的关系,公式为: Dice = 2 T P 2 T P + F P + F N \operatorname{Dice}=\frac{2TP}{2TP+FP+FN} Dice=2TP+FP+FN2TP 或 F 1 = 2 × P P V × T P R P P V + T P R \operatorname{F_1}=\frac{2×PPV×TPR}{PPV+TPR} F1=PPV+TPR2×PPV×TPR 是一个特殊值,其更一般的表示为 F-Score或 F-Measure: F − S c o r e = ( α 2 + 1 ) P P V × T P R α 2 P P V + T P R F-Score=(α^2+1)\frac{PPV×TPR}{α^2PPV+TPR} F−Score=(α2+1)α2PPV+TPRPPV×TPR 其中α为对TPR与PPV的加权求和。召回率与精确度一样重要时,令α=1,即为 F 1 F_1 F1;当认为精确度重要时,令α<1;反之认为召回率重要些时,则令α>1。
(specificity)也称 TNR(true negativerate),表示负样本被准确预测,公式为: S p e c i f i c i t y ( T N R ) = T N T N + F P Specificity(TNR)=\frac{TN}{TN+FP} Specificity(TNR)=TN+FPTN 特效度与误判率成反比,在检测中特效度低,则说明部分样本原本是负样本被模型误判成了缺陷。
(false positive rate, FPR),又称,: F P R = F P T N + F P FPR=\frac{FP}{TN+FP} FPR=TN+FPFP (false negative rate, FNR),又称,: F N R = F N T N + T P FNR=\frac{FN}{TN+TP} FNR=TN+TPFN (accuracy, ACC),一般情况下,ACC 越高模型越好,但样本不平衡时,ACC 不能很好地评估模型性能。 A C C = T P + T N T P + F P + T N + F N A C C=\frac{T P+T N}{T P+F P+T N+F N} ACC=TP+FP+TN+FNTP+TN (balanced accuracy,BA): B A = F N T N + T P BA=\frac{FN}{TN+TP} BA=TN+TPFN ( Matthews correlation coefficient, MCC)综合了 TPR、TNR、FPR、FNR,是一种比较全面的指标,可以评估样本不平衡下的缺陷检测模型性能。 M C C = T P × T N − F P × F N ( T P + F P ) ( T P + F N ) ( T N + F P ) ( T N + F N ) M C C=\frac{T P \times T N-F P \times F N}{\sqrt{(T P+F P)(T P+F N)(T N+F P)(T N+F N)}} MCC=(TP+FP)(TP+FN)(TN+FP)(TN+FN) TP×TN−FP×FN (mean average precision)是指各个类别预测正确的样本数占总样本数的平均值,越大越好。mAP 中的“AP(average precision)”是指平均精确度。当n=2时,则为二分类问题。当遇到多分类问题时n=类别数+1,因为需要加上背景。 m A P = ∑ P P V n mAP=\frac{\sum PPV}{n} mAP=n∑PPV (pixel accuracy, ),常用于语义分割判断分对的像素数量占总像素数量的比率: P A = ∑ i = 0 k p i i ∑ i = 0 k ∑ j = 0 k p i j P A=\frac{\sum_{i=0}^{k} p_{i i}}{\sum_{i=0}^{k} \sum_{j=0}^{k} p_{i j}} PA=∑i=0k∑j=0kpij∑i=0kpii (mean pixel accuracy, ),是对 PA 求平均。 m P A = 1 k + 1 ∑ i = 0 k p i i ∑ i = 0 k p i j m P A=\frac{1}{k+1} \sum_{i=0}^{k} \frac{p_{i i}}{\sum_{i=0}^{k} p_{i j}} mPA=k+11i=0∑k∑i=0kpijpii (mean intersection over union, )表示标注的准确性。 m I o U = 1 k + 1 ∑ i = 0 k p i i ∑ i = 0 k p i j + ∑ j = 0 k p j i − p i i m I o U=\frac{1}{k+1} \sum_{i=0}^{k} \frac{p_{i i}}{\sum_{i=0}^{k} p_{i j}+\sum_{j=0}^{k} p_{j i}-p_{i i}} mIoU=k+11i=0∑k∑i=0kpij+∑j=0kpji−piipii PA、mPA、mIoU 都为判断语义分割准确率的指标,其中 k 为总类别数, k+1 为加上背景, P i j P_{ij} Pij为第 i i i类像素被判为 j j j类的数量, 标签: 二极管pj3306q24j4pj连接器二极管后面带tp