电子罗盘(1)倾斜补偿:地磁场、磁传感器、倾斜补偿
地磁场和磁传感器
地磁场可用于获取定位信息。以北半球为例,地磁场的方向不是与地面水平,而是与水平方向有一定的倾角(指向地面),称为磁倾角(Inclination)。同时,地磁场的方向也不同于地理北方。两者的夹角称为磁偏角(Declination)。地磁场的磁感应强度约为30~70uT,与所在地有关。
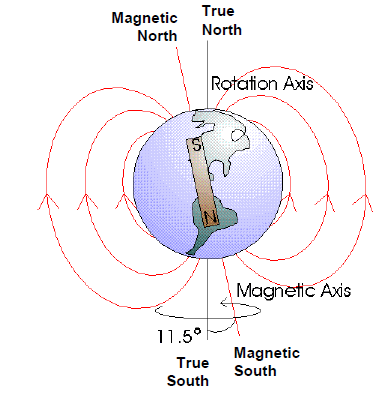
例如,根据以下网站,上海的磁偏角约为-6°,磁倾角约为47°,磁感应强度49.1uT(水平方向33uT,垂直方向36uT)。
World Magnetic Model Calculator (bgs.ac.uk)
(在后面的介绍中忽略磁倾角,假设磁北就是地理北。一般可以通过当地经纬度查询到磁偏角并加以换算)
一般有地磁传感器XY两轴或者XYZ基于霍尔效应或磁阻效应应或磁阻效应,用于手机、无人机等,实现电子罗盘功能。例如,可以测量两轴磁传感器XY通过简单的计算,在两个方向上获得磁感应强度。假设磁传感器XY平面保持水平,X轴读数hx,Y轴读数hy,设备的X轴方向和磁北的夹角是 θ = a t a n 2 ( h y h x ) \theta=atan2(\frac{h_y}{h_x}) θ=atan2(hxhy),θ范围是(-180°,180°]。
| hx | hy | θ |
|---|---|---|
| 0 | 0 | |
| (0,90°) | ||
| 0 | 90° | |
| - | (90°,180°) | |
| - | 0 | 180° |
| - | - | (-180°,-90°) |
| 0 | - | -90° |
| - | (-90°,0) |
2D和3D的旋转
磁场在某一位置的方向相对恒定,但磁传感器的姿态发生了变化,因此磁传感器各方向的读数与姿态有关。如下图所示MPU-6500,磁传感器的姿态可以绕过XYZ以逆时针旋转(从x轴箭头看箭尾)为正,表示三轴旋转。
例如,绕着Z轴旋转,Z轴读数不变,仅改变X轴和Y轴的读数。
原读数: v 0 = [ h x , h y ] T = [ H c o s θ , H s i n θ ] T v0=[h_x,h_y]^T=[Hcos\theta, Hsin\theta]^T v0=[hx,hy]T=[Hcosθ,Hsinθ]T 根据示意图,XY逆时针旋转 δ \delta δ后的读数: v ′ = [ h x ′ , h y ′ ] T = [ H c o s ( θ − δ ) , H s i n ( θ − δ ) ] T = [ H c o s θ c o s δ + H s i n θ s i n δ , H s i n θ c o s δ − H c o s θ s i n δ ] v'=[h_x',h_y']^T=[Hcos(\theta - \delta),Hsin(\theta - \delta)]^T=[Hcos\theta cos\delta+Hsin\theta sin\delta, Hsin\theta cos\delta - Hcos\theta sin\delta] v′=[hx′,hy′]T=[Hcos(θ−δ),Hsin(θ−δ)]T=[Hcosθcosδ+Hsinθsinδ,Hsinθcosδ−Hcosθsinδ] 这种旋转可以用矩阵表示: v ′ = [ c o s δ s i n δ − s i n δ c o s δ ] [ H c o s θ H s i n θ ] = R z 2 d ( δ ) v 0 v' = \left[ \begin{matrix} cos\delta & sin\delta \\ -sin\delta & cos\delta \end{matrix} \right] \left[ \begin{matrix} Hcos\theta \\ Hsin\theta \end{matrix} \right] = R_{z2d}(\delta)v_0 v′=[cosδ−sinδsinδcosδ][HcosθHsinθ]=Rz2d(δ)v0
然后把Z轴补上,变成一个3x3的矩阵(因为Z轴读数不变,所以只有3,3的元素是1,其他都是0): R z ( ψ ) = [ c o s ψ s i n ψ 0 − s i n ψ c o s ψ 0 0 0 1 ] R_z(\psi)= \left[ \begin{matrix} cos\psi & sin\psi & 0\\ -sin\psi & cos\psi & 0 \\ 0 & 0 & 1 \end{matrix} \right] Rz(ψ)=⎣⎡cosψ−sinψ0sinψcosψ0001⎦⎤ 同理,围绕X轴和Y轴旋转,对应的矩阵为: R x ( ϕ ) = [ 1 0 0 0 c o s ϕ s i n ϕ 0 − s i n ϕ c o s ϕ ] , R y ( θ ) = [ c o s θ 0 − s i n θ 0 1 0 s i n θ 0 c o s θ ] R_x(\phi)= \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & cos\phi & sin\phi\\ 0 & -sin\phi & cos\phi \end{matrix} \right], \; R_y(\theta)= \left[ \begin{matrix} cos\theta & 0 & -sin\theta \\ 0 & 1 & 0 \\ sin\theta & 0 & cos\theta \end{matrix} \right] Rx(ϕ)=⎣⎡1000cosϕ−sinϕ0sinϕcosϕ⎦⎤,Ry(θ)=⎣⎡cosθ0sinθ010−sinθ0cosθ⎦⎤
注意 R y ( θ ) R_y(\theta) Ry(θ)的 s i n θ sin\theta sinθ符号与其他两个矩阵不同,这与坐标轴设置有关,这里对应于上图MPU6500。
对于三轴磁传感器,定义一个初始位置:XY平面平行于水平面,同时X轴与地磁场方向重合。此时读数为: h 0 = [ H c o s I , 0 , H s i n I ] T h_0=[HcosI,0,HsinI]^T h0=[HcosI,0,HsinI]T。I是磁倾角。
-
如果只有Z轴的旋转,则读数变为: h r z = R z ( ψ ) h 0 = h r z = R z ( ψ ) h 0 = [ c o s ψ s i n ψ 0 − s i n ψ c o s ψ 0 0 0 1 ] [ H c o s I 0 H s i n I ] = [ H c o s I c o s ψ − H c o s I s i n ψ H s i n I ] h_{rz}=R_z(\psi)h_0= h_{rz}=R_z(\psi)h_0= \left[ \begin{matrix} cos\psi & sin\psi & 0\\ -sin\psi & cos\psi & 0 \\ 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} HcosI\\ 0 \\ HsinI \end{matrix} \right] = \left[ \begin{matrix} HcosIcos\psi \\ -HcosIsin\psi \\ HsinI \end{matrix} \right] hrz=Rz(ψ)h0=hrz=Rz(ψ)h0=⎣⎡cosψ−sinψ0sinψcosψ0001⎦⎤⎣⎡HcosI0HsinI⎦⎤=⎣⎡HcosIcosψ−HcosIsinψHsinI⎦⎤ 此时可以直接用 ψ = a t a n ( − h y h x ) \psi = atan(\frac{-h_y}{h_x}) ψ=atan(