学习笔记23--多传感器信息融合基础理论

• 要实现自动驾驶，需要多个传感器相互配合，共同构成自动驾驶汽车的感知系统；
• 在多传感器信息集成过程中，需要解决以下关键问题：
  • 数据对准。 由于每个传感器观察到的数据都在自己的参考框架内，因此在整合这些信息之前，必须将其交换到同一时空框架；必须补偿时空准备引起的舍入误差；
  • 传感器观测数据的不确定性。 由于传感器工作环境的不确定性，观测数据中存在噪声成分，这些信息的不确定性需要在整合过程中最大限度地降低；
  • 数据关联。 数据关联问题广泛存在，需要解决单传感器时间域和多传感空间域的关联问题，以确定来自同一目标源的数据；
  • 不完整、不一致和虚假数据。 在多传感器信息集成系统中，传感器接收到的测量数据有时有多种解释，称为数据不完整性；多传感器数据往往解释观测环境不一致甚至矛盾；
• 对车载系统的要求：
  • 统一同步时钟，确保传感器信息的时间一致性和正确性；
  • 多传感器校准准确，同时保证不同传感器信息的空间一致性；

• 传感器数据集成是针对系统使用各种传感器的信息处理方法，可以发挥各种传感器的联合优势，消除单个传感器的局限性；
• 把分布在不同位置的多个同类或不同类传感器所提供的数据资源加以综合，采用使计算机技术对其进行分析，加以互补，实现最佳协同效果，获得对被观测对象的一致性解释与描述，提高系统的容错性，从而提高系统决策、规划、反应的快速性和正确性，使系统获得更充分的信息；
• 多传感器融合技术优势：
  • 提高系统感知的准确性。 各种传感器相互补充，可以避免单个传感器的局限性，最大限度地发挥各传感器的优取被检测对象的各种特征信息，减少环境、噪声等干扰；
  • 增加系统的感知维度，提高系统的可靠性和强度。 多传感器集成可以带来一定的信息冗余。即使传感器出现故障，系统也能在一定范围内继续正常工作，容错性高，增加了系统决策的可靠性和可信度；
  • 提高环境使用能力。 采用多传感器集成技术收集的信息具有明显的互补性，覆盖了更广泛的空间和时间，弥补了单传感器对空间的分辨率和环境的语义不确定性。
  • 有效降低成本。 在保证性能的基础上，可以实现多个低成本传感器而不是昂贵的传感器设备；
• 传感器融合过程：
  1. 多个传感器独立工作获取观察数据；
  2. 每个传感器数据(RGB预处理图像、点云数据等。
  3. 对处理数据进行特征提取、变换，并进行模式识别处理，获取对观察对象的描述信息；
  4. 在数据融合中心按照一定的标准进行数据关联；
  5. 各传感器数据采用足够优化的算法集成，对观测对象进行一致性描述和解释。

将多传感器信息融合分为：Low-level融合、High-level融合与混合结构；

• Low-level集成：包括数据级融合和特征级融合，是集中融合结构；
• High-level一体化：一种决策级融合，可以是集中融合或分布式融合；
• 混合结构：多种Low-level和High-level由结构组合而成；

Low-level集成系统结构是信息水平较低的融合，是集中融合结构；集中式集成结构直接将传感器获得的原始数据发送到数据集成中心，进行数据对准、数据关联、预测等可实现传感器端的实时集成。 集中式集成结构集成精度高，算法灵活，但处理器要求高，计算量大，成本高，数据流量单一，底层传感器之间缺乏信息通信，可靠性低，难以实现；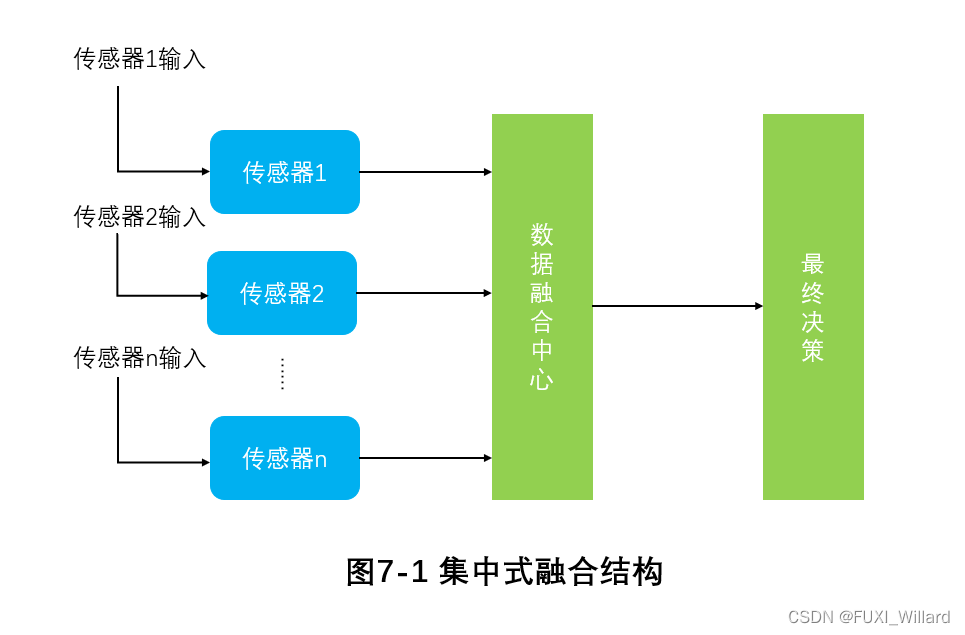

1. 数据级融合 数据级集成，又称像素级集成，是最低级集成，直接集成传感器的观测数据，然后根据集成结果提取和判断特征。
   • 数据级融合处理的数据是最底层数据，精确到图像像素级别，但计算量大，处理所耗费的时间成本巨大，不利于实时处理；在进行数据通信时，容易受不稳定性、不确定性因素的影响；其处理过程都是在同种传感器下进行，无法有效地处理异构数据；
   • 根据集成内容，数据级集成分为图像级融合、目标级融合和信号级融合。图像级集成以视觉为主体，转换雷达输出的整体信息，与视觉系统的图像输出集成；目标级集成是对视觉和雷达输出的综合可信度进行加权，并与精度校准信息进行自适应的搜索匹配；信号级集成是视觉和雷达传感器ECU数据损失小，可靠性高，但需要大量计算。
2. 特征级融合 特征级集成是指在提取收集到的数据中包含的特征向量后的集成。特征级集成通过各传感器的原始数据和决策推理算法对特征信息进行分类、收集和综合，提取具有表达能力和统计信息的属性特征。
   1. 特征级集成首先压缩图像信息，然后通过计算机进行分析和处理，消耗的内存、时间和数量级相对减少，从而提高处理的实时性；
   2. 特征级融合分为目标状态信息融合和目标特征融合；目标状态信息集成，首先配置数据，以实现状态和参数的估计，更适合目标跟踪；目标特征集成，利用传统模式识别技术，在特征预处理的前提下进行分类和组合。

High-level集成系统结构是一种高语义层次的集成，可以是分布式集成结构或集中式集成结构；分布式集成结构在独立节点设置相应的处理单元，在局部处理独立传感器获得的原始数据的基础上，将结果输入数据集成中心进行智能优化、组合和推理，以获得最终结果。 分布式集成结构计算速度快，连续性好，传感器故障时可继续工作，可靠性高；分布式集成结构对通信带宽要求低，适用于远程传感器信息反馈，但在低通信带宽中传输会造成一定的损失，降低精度。 集中式融合结构，根据不同种类的传感器对同一目标观测的原始数据，进行一定的特征提取、分类、判别，以及简单的逻辑运算，然后根据应用需求进行较高级的决策，获得简明的综合推断结果，是高语义层次上的融合。

多传感器融合常用算法：随机类和人工智能方法。随机类方法：卡尔曼滤波法(Kalman filtering)，加权平均法、贝叶斯估计法(Bayesian estimation)、D-S(Dempster-Shafer)证据理论等；人工智能方法：专家系统、模糊逻辑理论、人工神经网络、遗传算法等；