卡尔曼滤波器是利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据包括系统中噪声和干扰的影响，最佳估计也可视为滤波过程。数据滤波器是一种数据处理技术，可以去除噪声，恢复真实数据。当测量方差已知时，卡尔曼滤波器可以从一系列测量噪声的数据中估计动态系统的状态。

假设当前以位置和速度的状态做简单例子解释： a ? = [ p v ] \vec{a}=\begin{bmatrix} p \\ v \end{bmatrix} a =[pv]我们不知道实际的位置和速度，它们之间有很多正确的组合，但有些比其他部分更有可能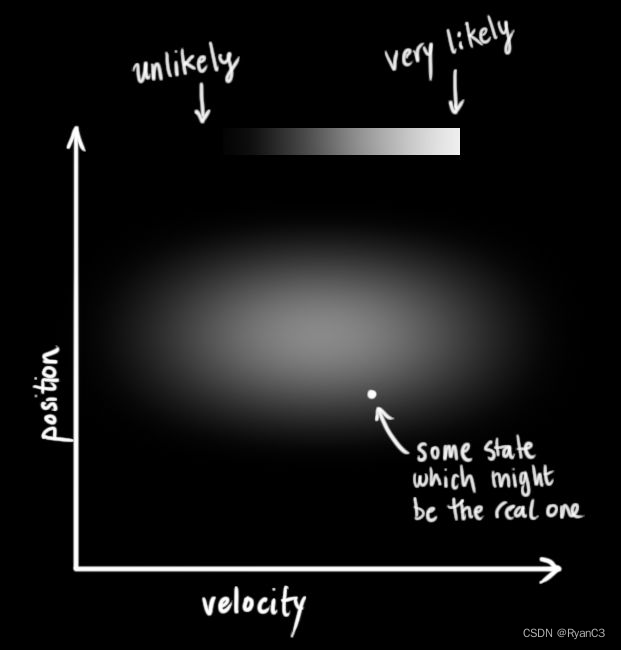： 在当前的例子中（如果没有特殊的解释，以下都是这个例子），卡尔曼滤波器假设两个变量是随机的，并服从高斯分布。每个变量都有一个平均值 μ \mu μ，中心表示随机分布和方差 σ 2 \sigma^2 σ2表示不确定性。 在上图中，位置和速度的关系是不相关的，这意味着由其中一个变量的状态无法推测出另一个变量可能的值。下面例子更有趣：位置和速度是相关的，观测特定位置的可能性取决于当前的速度： 这种情况是有可能发生的，例如，基于旧的位置来估计新位置。如果速度过高，物体可能已经移动很远了。如果缓慢移动，则距离不会很远。跟踪这种关系是非常重要的，因为他带给我们更多的信息：其中一个测量值告诉了其它变量可能的值，这就是卡尔曼滤波的目的，尽可能地在包含不确定性的测量数据中提取更多信息。 这种相关性用协方差矩阵来表示，简而言之，矩阵中的每个元素 ∑ i j \sum ij ∑ij表示第 i i i个和第 j j j个状态变量之间的相关度。（你可能已经猜到协方差矩阵是一个对称矩阵，这意味着可以任意交换 i 和 j）。协方差矩阵通常用“ ∑ \sum ∑”来表示，其中的元素则表示为“ ∑ i j \sum ij ∑ij”。

基于高斯分布建立状态变量，所以在时刻 k k k需要两个信息，最佳估计 X k X_k Xk​，即均值，以及协方差矩阵 P k P_k Pk​ 需要根据当前状态（ k − 1 k-1 k−1时刻）来预测下一状态（ k k k时刻）。我们不知道对下一状态的所有预测中哪个是“真实”的，但预测函数并不在乎。它对所有的可能性进行预测，并给出新的高斯分布。 可以用矩阵 F k F_k Fk​来表示这个预测过程： 它将我们原始估计中的每个点都移动到了一个新的预测位置，如果原始估计是正确的话，这个新的预测位置就是系统下一步会移动到的位置。下面用一个基本的运动学公式来表示如何用矩阵来预测下一个时刻的位置和速度： 现在，已经可以通过一个预测矩阵来表示下一时刻的状态，但是，仍然不知道怎么更新协方差矩阵。此时，需要引入另一个公式，如果将分布中的每个点都乘以矩阵 A，那么它的协方差矩阵 ∑ \sum ∑会怎样变化呢？很简单，下面给出公式： 结合方程（3）和（4）得到：

我们并没有捕捉到一切信息，可能存在外部因素会对系统进行控制，带来一些与系统自身状态没有相关性的改变。 以火车的运动状态模型为例，火车司机可能会操纵油门，让火车加速。相同地，在我们机器人这个例子中，导航软件可能会发出一个指令让轮子转向或者停止。如果知道这些额外的信息，我们可以用一个向量 Uk 来表示，将它加到我们的预测方程中做修正。 假设由于油门的设置或控制命令，我们知道了期望的加速度 a a a，根据基本的运动学方程可以得到： B k B_k Bk​称为控制矩阵， U k U_k Uk​称为控制向量（对于没有外部控制的简单系统来说，这部分可以忽略）。让我们再思考一下，如果我们的预测并不是100%准确的，该怎么办呢？

可能会有多个传感器来测量系统当前的状态，哪个传感器具体测量的是哪个状态变量并不重要，也许一个是测量位置，一个是测量速度，每个传感器间接地告诉了我们一些状态信息。 注意，传感器读取的数据的单位和尺度有可能与我们要跟踪的状态的单位和尺度不一样，我们用矩阵Hk 来表示传感器的数据。 可以计算出传感器读数的分布，用之前的表示方法如下式所示： 卡尔曼滤波的一大优点就是能处理传感器噪声，换句话说，我们的传感器或多或少都有点不可靠，并且原始估计中的每个状态可以和一定范围内的传感器读数对应起来。 从测量到的传感器数据中，我们大致能猜到系统当前处于什么状态。但是由于存在不确定性，某些状态可能比我们得到的读数更接近真实状态。 将这种不确定性（例如：传感器噪声）用协方差 R k R_k Rk​表示，该分布的均值就是我们读取到的传感器数据，称之为 Z k Z_k Zk​ 。现在我们有了两个高斯分布，一个是在预测值附近，一个是在传感器读数附近。 必须在预测值（粉红色）和传感器测量值（绿色）之间找到最优解。那么，最有可能的状态是什么呢？对于任何可能的读数 ( z 1 z_1 z1​, z 2 z_2 z2​) ，有两种情况：（1）传感器的测量值；（2）由前一状态得到的预测值。如果我们想知道这两种情况都可能发生的概率，将这两个高斯分布相乘就可以了。 剩下的就是重叠部分了，这个重叠部分的均值就是两个估计最可能的值，也就是给定的所有信息中的最优估计。这个重叠的区域看起来像另一个高斯分布。 把两个具有不同均值和方差的高斯分布相乘，你会得到一个新的具有独立均值和方差的高斯分布！下面用公式讲解。

先以一维高斯分布来分析比较简单点，具有方差 σ 2 \sigma^2 σ2和 μ \mu μ的高斯曲线可以用下式表示： 将式（9）代入到式（10）中（注意重新归一化，使总概率为1）可以得到： 将式（11）中的两个式子相同的部分用 k k k表示：

下面进一步将式（12）和（13）写成矩阵的形式，如果 ∑ \sum ∑表示高斯分布的协方差， μ \mu μ表示每个维度的均值，则： 矩阵 K K K称为卡尔曼增益。将所有公式整合起来，有两个高斯分布，预测部分和测量部分，将它们放到式（15）中算出它们之间的重叠部分： 由式（14）可得卡尔曼增益为： 将式（16）和式（17）的两边同时乘矩阵的逆得到以下等式：

上式给出了完整的更新步骤方程。 X k ′ X_k' Xk′​就是新的最优估计，我们可以将它和 P k ′ P_k' Pk′​放到下一个预测和更新方程中不断迭代。