https://blog.csdn.net/qq_41821067/article/details/115358983

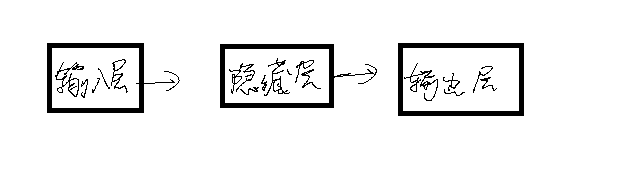输入层不处理数据，不计入层数。隐藏层可以有一层或多层。输出层是最后一层。输出层的格式根据不同的需要而有所不同。

网络训练中用到了数学，统计学，最优化等众多学科。

这里我们提到了量化处理，那么什么是量化处理，就是按照归一化、白化、灰度化、嵌入等一定的规则编码。

每个网络都相当于一个函数g(x|Θ),为下标表示，以区分不同的网络层，如g1(x|Θ1)，g2(x|Θ2.)… 要解决的问题是f(x|Θ)中的Θ取什么值，每层中的gi(x|Θi)如果确定了这些值，可以进行训练

训练者自己定义了损失函数，表示模型误差的大小，

解决损失函数极小值的过程是训练过程，

模型训练后，模型开始工作。即将输入值代入训练好的模型函数，获得输出值。这个过程很简单，因为它只是一个简单的加减乘除操作。 这也得到了很多训练时间长、反向传播的过程，工作是样本正向传播的过程。

我们通常接触到的损失函数包含许多项目

在没有非线性函数之前，我们使用传统的机器分类模型，如贝叶斯、决策树和支持向量机进行机器学习。提取特性是一个重要环节，

多层线性分类器模拟的堆叠 SVM神经网络的每一个神经元都是经网络的每一个神经元都是线性分类器， 如何对上述四边形进行分类，一边是四边形内点，另一边是四边形外点。我们使用四条直线（红线），即四个线性分类器进行分类。 因为神经网络有很多层，每层都有很多神经元，一个神经元可以被视为线性分类器，所以线性不可分割的模型可以被分类。 随着维度和深度的增加，分类器将变得越来越复杂，可以与线性分类器叠加，或，非。

宽度归一化

只要我们输入数据样本，机器就会通过输入图片的向量特征和f(x|Θ)中的Θ进行计算。

import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms


# Device configuration
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

# Hyper-parameters 
input_size = 784
hidden_size = 500
num_classes = 10
num_epochs = 5
batch_size = 100
learning_rate = 0.001

# MNIST dataset 
train_dataset = torchvision.datasets.MNIST(root='../../data', 
                                           train=True, 
                                           transform=transforms.ToTensor(),  
                                           download=True)

test_dataset = torchvision.datasets.MNIST(root='../../data', 
                                          train=False, 
                                          transform=transforms.ToTensor())

# Data loader
train_loader = torch.utils.data.DataLoader(dataset=train_dataset, 
                                           batch_size=batch_size, 
                                           shuffle=True)

test_loader = torch.utils.data.DataLoader(dataset=test_dataset, 
                                          batch_size=batch_size, 
                                          shuffle=False)

# Fully connected neural network with one hidden layer
class NeuralNet(nn.Module):
    def __init__(self, input_size, hidden_size, num_classes):
        super(NeuralNet, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size) 
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(hidden_size, num_classes)  
    
    def forward(self, x):
        out = self.fc1(x)
        out = self.relu(out)
        out = self.fc2(out)
        return out

model = NeuralNet(input_size, hidden_size, num_classes).to(device)

# Loss and optimizer
#使用交叉熵损失，损失函数的值就是在一个epoch中在每个样本上的平均误差值。
criterion = nn.CrossEntropyLoss()
#优化方法为Adam，类似随机梯度下降，使得整个网络中的待定系数朝着减小整个误差值的方向进行
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)  

# Train the model
#总步长是加载数据的长度total_step
total_step = len(train_loader)
for epoch in range(num_epochs):
    for i, (images, labels) in enumerate(train_loader):  
        # Move tensors to the configured device
        #正向传播一幅图片并得到一个拟合值
        images = images.reshape(-1, 28*28).to(device)
        labels = labels.to(device)
        
        # Forward pass
        outputs = model(images)
        # 计算损失函数的值
        loss = criterion(outputs, labels)
        
        # 反向传播并进行优化
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        
        if (i+1) % 100 == 0:
            print ('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}' 
                   .format(epoch+1, num_epochs, i+1, total_step, loss.item()))

# Test the model
# In test phase, we don't need to compute gradients (for memory efficiency)
with torch.no_grad():
    correct = 0
    total = 0
    for images, labels in test_loader:
        images = images.reshape(-1, 28*28).to(device)
        labels = labels.to(device)
        outputs = model(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

    print('Accuracy of the network on the 10000 test images: {} %'.format(100 * correct / total))

# Save the model checkpoint
torch.save(model.state_dict(), 'model.ckpt')

机器学习中用来衡量样本量的一个词，如在机器学习中准备了50000个样本，当全部样本通过网络进行了一次正向传播的时候就叫做一个epoch,在上面代码中batch-size=100,也就是随机挑选100个样本进行训练，再进行一次梯度下降，每处理一批(batch)样本就叫做一个step,要让50000个样本通过网络完成一个epoch就要500个step 1次epoch完成的样本=step*batch_size 注意！batch从样本中抽取就不能放回。

可以由我们自己确定，让每个样本都能等权重地在训练中发挥作用，让每个样本都有同等的机会进行正向传播并产生相应的损失值。

我们只需要把数据找到，把网络搭好，把损失函数定义好，其他就可以交给计算机了，不用手动进行分类。