论文名:
摘要:
Alexnet在当时的cv算法主要以低误差为优点。
其中使用ImageNet数据集,数据集的内容及其巨大,大部分参考只使用了120万(全部使用效果更好,但部分参考对结果的影响忽略不计)。
主要用于5卷积层和3卷全连接层。
为了加快训练速度,使用了非饱和神经元而且很有效 GPU实现卷积操作。
为减少全连接层中的过度拟合,采用了开发的名称==“dropout正则化方法==,这种方法被证明是非常有效的(因为这篇文章具有划时代的意义,很多结论现在都不适用,这里dropout此外,由于目前的全连接层意义重大gpu技术改进,以前不再使用多种训练方法进行一些训练gpu)。
内容
-
数据集
ImageNet数据集是由不同分辨率的图像组成,而系统需要固定的输入尺寸。这里采用的方法是:给定一个矩形图像,首先依据最短的那条边重新缩放图像,使其缩放到256,然后从得到的图像中裁剪出中央的256x256元。除了从每个像素中减去训练集的平均活动外,没有其他方法预处理图像
-
搭建过程
-
发现Relu比tanh要好
-
在多个GPU训练(现在不能成为主流)
-
局部反应归一化(论文提出的公式目前不再使用)
-
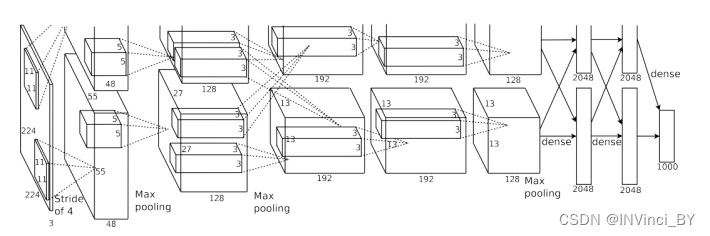
明确划分两个GPU职责之间的划分,同时规定在某些层面进行通信
-
-
减少过度拟合:
-
数据增强:人工扩展数据集采用标签保护的转换(常用方法有:随机水平转换、尺度转换、随机垂直转换、平移转换、噪声扰动、镜像转换)
本文采用两种形式:(1)包括图像的平移和水平反射(2)包括训练图像的变化RGB具体来说,通道的强度是训练集RGB像素值进行PCA( 详细说明主成分分析 ——在每个训练图像中训练图像中添加发现的主要成分倍数。
-
-
细节
采用SDG(随机梯度下降法)训练模型。学习率初始化为0.01(一般规则)可以使用更平滑的方法,即在整个培训过程中手动调整所有层的相同学习率。当验证错误率不再随当前学习率而提高时,也可以使用启发性方法将学习率除以10。
最后
本论文采用有监督学习方法,当时那种以无监督学习作为主流时代具有特殊意义。作者希望在视频序列中使用非常大的深度卷积网络。
--分界线--
附录:
-
监督学习和无监督学习
监督学习: 从给定的训练数据中学习函数(模型参数),当新数据到来时,可以根据函数预测结果。
无监督学习: 输入数据没有标记,也没有确定的结果。样本数据类别未知,样本集需要根据样本之间的相似性进行分类(聚类,clustering)试图最大限度地差距,最大化类间差距。
-
饱和神经元
- non-saturating neurons (非饱和神经元)= 处理过的值未被挤压(到特定范围)。
- saturating neurons (饱和神经元)= 挤压过的值(到特定范围)
与神经元对应的有non-linear activation,这里non-linear activation分为两类:
- 输出饱和神经元的激活函数:
- sigmoid: input neurons该值被挤压到[0,1]的范围
- tanh:input neurons该值被挤压到[-1,1]的范围
- 激活函数输出非饱和神经元
- relu:input neurons值,或0, 或保持原值(无挤压,无最大最小值限制)
- leaky_relu:input neurons的值, 或按一定比例缩小,或保持原值(无挤压,无最大最小值限制)
-
全连接层
全连接层在卷积神经网络中起着分类器的作用。如果卷积层、池化层、激活函数等操作将原始数据映射到隐藏特征空间,则全连接层将所学的分布式特征表示映射到样本标记空间中
-
PCA主成分分析
PCA主要思想是,k维特征是在原n维特征的基础上重构的。
步骤:
-
样本归0:将样本的平均值归0,即所有样本减去样本的平均值。样本的分布没有改变,只是移动了坐标轴。
此时的方差公式为0
-
找到样本点映射后方差最大的单位向量ω,转化为目标函数的优化: V a r ( X p r o j e c t ) = 1 m ∑ i = 1 m ( X ( i ) ? ω ) 2 Var(X_{project})= \frac{1}{m} \sum^m_{i=1}(X^{(i)}·ω)^2 Var(Xproject)=
m1 i=1∑m(X(i)⋅ω)2 -
求 ω 使公式(1)最大
-
利用算法梯度法求解
在求极值的问题中,有梯度上升和梯度下降两个最优方法,梯度上升用于求最大值,梯度下降用于求最小值
使损失函数变小的迭代公式: ( a k + 1 , b k + 1 ) = ( a k + 1 − η ∂ L ∂ a , b k + 1 − η ∂ L ∂ b ) (a_{k+1},b_{k+1}) =(a_{k+1}-η \frac{∂L}{∂a},b_{k+1}-η \frac{∂L}{∂b}) (ak+1,bk+1)=(ak+1−η∂a∂L,bk+1−η∂b∂L)
-
-
Dropout正则化
它不仅防止了过度拟合,并提供了一种有效地以指数级方式组合许多不同的神经网络体系结构的方法 。
dropout是指在训练模型时,神经网络随机(以一定的概率)丢弃一些神经元
丢弃神经元:意味着在神经网络中“临时”的将其和与其相连的全部输入和输出链接删除。
在一般解决过程中,主要通过两种方法进行解决或改善:
- 丢弃一些不能帮助我们正确预测的特征。(例如:PCA)
- 正则化。保留所有特征,但是减少参数的大小
Dropout比较流行的实现主要有两种类型:Vanilla Dropout 和Inverted Dropout
其中Vanilla Dropout是朴素实现版本,而Inverted Dropout是更加广为使用和流行的实现。
:具体应用在深度神经网络的中间隐藏层,对于某一层L,如果应用了概率p的Dropout,在网络的训练/测试中,每个神经元都有p的概率会被“丢弃”,即该神经元不参与权重矩阵的计算。
模型训练时应用Dropout的流程,概况是:
- 随机概率p随机dropout部分神经元,并向前传遍
- 计算前向传播的损失,应用反向传播和梯度更新(对剩余的未被dropout的神经元)
- 恢复所有神经元,并重复过程1
**Inverted Dropout:**在训练节点,同样应用p的概率来随机失活,不过额外提前除以1-p,这样相当于将网络的分布提前“拉伸”,好处就是在预测阶段,网络无需再乘以1-p来压缩分布
# -*- coding = utf-8 -*- # @Time : 2022/7/27 14:35 # @Author : Vinci # @File : f_dropout.py # @Software: PyCharm import torch def dropout(X, drop_prob): X = X.float() assert 0 <= drop_prob <= 1 keep_prob = 1 - drop_prob if keep_prob == 0: return torch.zeros_like(X) mask = (torch.rand(X.shape) < keep_prob).float() Y = mask * X / keep_prob return Y if __name__ == "__main__": X = torch.arange(16).resize(2, 8) print(dropout(X, 0.2) * 0.8)