本章将所有机器人建模成刚体连杆。
2.1 自由度计算
对于机器人来说,首先要注意的是它在哪里?如何描述机器人的位置非常简单,即描述机器人上的每个点。由于机器人的连杆刚性,形状已知,只需几个坐标即可描述。如图所示,铰链角度可用于门的位置θ来描述。 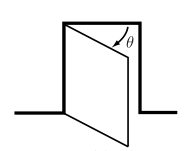
两个坐标可用于平面上某一点的位置(x, y)用三个坐标来描述硬币正面朝上的位置:两个坐标(x, y)表示硬币上某一点的位置和角度θ表示硬币的朝向。这些坐标都在连续的实数域内取值。
由此,我们引出自由度的定义,机器人的自由度(dof)表示位形所需的最小实值坐标数。
在我们上面的描述中,门有一个自由度,硬币有三个自由度。这里需要注意的是,硬币虽然有两种前后状态,但前后是一个离散的集合,而不是一个连续的实数空间。
这样,本章的第一个定义就出现了,加粗部分是C空间的定义:
: The configuration of a robot is a complete specification of the position of every point of the robot. The minimum number n of real-valued coordinates needed to represent the configuration is the number of degrees of freedom (dof) of the robot.
接下来,我们将探索刚体的自由:
以桌面上的硬币为例,选择三点A、B、C,建立直角坐标系o-xy,如果这些点可以独立放置在平面上的任何位置,硬币将有6个自由度-3个点,每个点有2个自由度。A、B、C三点之间的距离是一个定值,其坐标为: ( x A , y A ) , ( x B , y B ) , ( x c , y c ) \left( x_A,y_A \right),\left( x_B,y_B\right) ,\left( x_c,y_c\right) (xA,yA),(xB,yB),(xc,yc).
他们满足以下关系: d ( A , B ) = ( x A − x B ) 2 + ( y A − y B ) 2 = d A B , d ( B , C ) = ( x B − x C ) 2 + ( y B − y C ) 2 = d B C , d ( A , C ) = ( x A − x C ) 2 + ( y A − y C ) 2 = d A C . \begin{array}{l} d(A, B)=\sqrt{\left(x_{A}-x_{B}\right)^{2}+\left(y_{A}-y_{B}\right)^{2}}=d_{A B}, \\ d(B, C)=\sqrt{\left(x_{B}-x_{C}\right)^{2}+\left(y_{B}-y_{C}\right)^{2}}=d_{B C}, \\ d(A, C)=\sqrt{\left(x_{A}-x_{C}\right)^{2}+\left(y_{A}-y_{C}\right)^{2}}=d_{A C} . \end{array} d(A,B)=(xA−xB)2+(yA−yB)2 =dAB,d(B,C)=(xB−xC)2+(yB−yC)2 =dBC,d(A,C)=(xA−xC)2+(yA−yC)2 =dAC. 要确定硬币的自由度数,首先选择A点的坐标 ,这样由于约束条件,B点就只能在以A点为圆心的圆上,此时B相对于A位置的确定仅仅只需要B相对于A的夹角θ即可,一旦A和B的坐标都确定,那这样C点的位置就有两种情况,在以A点为圆心的圆以及和B点为圆心的圆的交点处,这恰好对应着硬币为正反面的两个位置,由此,硬币在平面上有三个自由度,即 ( x , y , θ ) (x,y,\theta) (x,y,θ)。
如果我们在硬币上再选择一点D,重复上述的计算过程,可以很容易得出引入的D点坐标将被消掉,因此没必要再去考虑别的点。
那么对于确定刚体系统的自由度数,有没有什么通用的计算方法呢,常用的规则如下: d e g r e e s o f f r e e d o m = ( s u m o f f r e e d o m s o f t h e p o i n t s ) − ( n u m b e r o f i n d e p e n d e n t c o n s t r a i n t s ) degrees\ of\ freedom =(sum\ of\ freedoms\ of\ the\ points)-(number\ of\ independent\ constraints) degrees of freedom=(sum of freedoms of the points)−(number of independent constraints) 这个规则也可以用描述系统的变量和独立方程的数量来表示: d e g r e e s o f f r e e d o m = ( n u m b e r o f v a r i a b l e s ) − ( n u m b e r o f i n d e p e n d e n t e q u a t i o n s ) degrees \ of\ freedom = (number\ of\ variables)-(number\ of \ independent\ equations) degrees of freedom=(number of variables)−(number of independent equations) 很明显硬币的例子就可以用系统的变量数目6减去独立方程的数目3得到,在平面上放置的硬币的自由度为3.
上述规则还可以推广用于确定三维空间中刚体的自由度,依旧以硬币为例,假设其在空间内任意位置,那这样依旧使用规则进行计算,系统的独立变量数目为9减去独立方程的数目3,那么在空间中的硬币的自由度为6.
通过上述例子,在三维空间中的刚体,称为spatial rigid body,有6个自由度,在二维平面中的刚体,称为planar rigid body,有3个自由度,在二维平面中的刚体可以看成是空间6自由度的刚体附加了 z a = z b = z c = 0 z_a=z_b=z_c=0 za=zb=zc=0 ,也可以是其余两个参数)的约束。
由上述的两个规则,就可以得到确定一般机器人自由度的规则: d e g r e e s o f f r e e d o m = ( s u m o f f r e e d o m s o f t h e b o d i e s ) − ( n u m b e r o f i n d e p e n d e n t c o n s t r a i n t s ) degrees\ of\ freedom = (sum\ of\ freedoms\ of\ the\ bodies) -(number\ of\ independent\ constraints) degrees of freedom=(sum of freedoms of the bodies)−(number of independent constraints) 了解了刚体系统自由度的计算,下面我们进入机器人自由度的计算:
再次考虑一开始提到的的门的例子,门由一个单一刚体通过铰链连接到墙壁。很容易看出门只有一个自由度,用铰链接的角度来表示。如果没有铰链,门就可以在三维空间中自由移动,有6个自由度,通过铰链将门与墙连接,门的运动受到五个独立约束,只能转动,也可以这样理解或者,门可以从上面看,视为一个平面体,有三个自由度。然后铰链关节施加两个独立的约束,只有一个独立的坐标。
上述的描述我们可以看出,铰链的存在使得自由度降低了,对于主要由关节和连杆组成的机器人来说,能否通过计算关节和连杆数目确定机器人的自由度呢,答案是肯定的,这就是用于计算机器人自由度的$\text { Grübler’s formula} $.
在进入公式之前,我们需要了解机器人中都有哪些关节:
各关节的自由度数和约束数目如下表所示:
有了这些,我们就可以开始介绍来计算机器人的自由度,废话不多说,上公式:
注意:本公式只有在所有关节约束都是独立的情况下才成立。如果它们不是独立的,那么公式就提供了自由度数目的下界。
说实话,看这英文是否大家都很懵圈,因此推荐大家去看孙恒,陈作模,葛文杰.机械原理(第八版)[M].高等教育出版社,2013:195-260,第2章第5节:机构自由度的计算,空间机构自由度计算公式为: F = 6 n − ∑ i = 1 5 i p i F=6 n-\sum_{i=1}^{5} \mathrm{ip}_{\mathrm{i}} F=6n−i=1∑5ipi 式中n为活动构件数,即机构的构件数N减去机架, N = n − 1 N=n-1 N=n−1, p i p_i pi为 i i i级副的个数, i i i为 i i i级副的约束数目,看下面几张图:
是不是和英文文献的表很相似,这样中英文的公式就对上了,下面用一个例子来展示如何计算:
这是一个仿人机械臂,那由人的身体结构可以得到,肩关节和腕关节为球面副,肘关节为球销副,以人体肩部为机架,那么我们使用公式来进行计算:
活动构件数n为4-1=3,球面副按照图可知是三级副,球销副是四级副,那么就有两个三级副,1个四级副,几级副就意味着有几个约束,那么四级副有4个约束,自由度,6-4=2,同理三级副就是3,这样代入公式可得,仿人机械臂的自由度为:6x3-2x1-3x2=8
自由度为8>6表示仿人机械手运动的灵活度较高,有很好的绕障工作能力。
通过上述例题,空间自由度的计算是否就很简单了呢,只需要知道活动构件数,几级副的数目再结合几何结构就可以很方便算出。
2.2 拓扑学
拓扑学部分,这里着实抽象,高能预警:
接下来探讨C空间的拓扑结构和表示,之前的讨论,一直在关注机器人自由度数。然而,C空间的形状拓扑结构也很重要。
考虑一个在球面上移动的点。点的C空间是二维的,因为点的位置可以用纬度和经度两个坐标来描述。对于在平面上移动的点,也有一个二维的C空间,即坐标(x, y)。显而易见,虽然一个平面和一个球体的表面都是二维的,但平面无限延伸,而球体环绕包裹。
与平面不同的是,一个较大的球体与原来的球体有着相同的形状,因为它们以相同的方式环绕,仅仅只是直径不同。椭圆形的橄榄球也类似于球形,橄榄球和球体之间的区别是橄榄球是球体向一个方向拉伸产生的。
实线的开区间(a, b)可以变形为开半圆,通过下图所示的做法,这个开放的半圆也可以变形为真实的直线即从半圆中心的一点开始,画一条与半圆相交的射线,然后在半圆上方画一条线,这些射线表明,半圆上的每一点都可以拉伸到直线上的一点,反之亦然。因此,开区间可以连续变形为直线,开区间和直线在拓扑上是等价的。
小球体、大球体和足球的二维表面都有相同的形状,但其余平面的形状是不同的,这种想法是通过表面的拓扑来表达的。在这本书中,不进行严格的处理,如果一个空间可以在不切割或粘合的情况下不断变形成另一个空间,那么这两个空间在拓扑上是等价的。球体可以简单地通过拉伸变形成橄榄球,而不需要切割或粘合,因此这两个空间在拓扑上是等价的。但是,你不能在不切割球体的情况下把它变成平面,所以球面和面在拓扑上是不相等的。
拓扑上不同的一维空间包括圆、直线和直线的闭合区间。圆被数学的描述为 S S S或 S 1 S^1 S1,即一维球面,线被写作 E E E或 E 1 E^1 E1,表示一维的欧几里德(或"平坦")空间,因为 E 1 E^1 E1中的点通常用实数表示(在选择原点和长度尺度之后),所以它通常写成 R R R或 R 1 R^1 R1,包含其端点的直线的闭区间可以写成[a,b]包含于 R 1 R^1 R1 ,开区间(a, b)不包括端点a和b,拓扑上等同于一条线,因为开区间可以拉伸成一条线,如图所示。
闭区间在拓扑上不等同于直线,因为直线不包含端点。
在高维中, R n R^n Rn 是n维欧几里德空间, S n S^n S<