• 自动驾驶规划控制概述
• A Survey of Motion Planning and Control Techniques for Self-Driving Urban Vehicles
• https://zhuanlan.zhihu.com/p/46377932
• pythonRobotics
• Frenet整理坐标推导过程
• Frenet学习坐标系相关知识系统
• 反馈后轮位置
• 后轴反馈控制——frenet坐标的应用

后轮反馈控制（Rear wheel feedback）是利用后轮中心的跟踪偏差计算转向控制量的方法。

如图所示，参考轨迹上最接近车辆后轴中心的点 ( x r e f , y r e f ) (x_{ref},y_{ref}) (xref,yref)为： s ( t ) = arg min γ ∥ ( x r ( t ) , y r ( t ) ) ? ( x r e f ( γ ) , y r e f ( γ ) ) ∥ (1) \tag{1} s(t)=\arg \min _{\gamma}\left\|\left(x_{r}(t), y_{r}(t)\right)-\left(x_{r e f}(\gamma), y_{r e f}(\gamma)\right)\right\| s(t)=argγmin ∥ (xr​(t),yr​(t)) − (xref​(γ),yref​(γ)) ∥ (1) 其中， ( x r ( t ) , y r ( t ) ) \left(x_{r}(t), y_{r}(t)\right) (xr​(t),yr​(t)) 代表 t t t 时刻车辆后轴中心位置坐标， ( x r e f ( γ ) , y r e f ( γ ) ) \left(x_{r e f}(\gamma), y_{r e f}(\gamma)\right) (xref​(γ),yref​(γ)) 代表参考路径上离车辆后 轴距离最近点的位置坐标， s ( t ) s(t) s(t) 代表 t t t 时刻与车辆后轴中心点距离最近参考轨迹点的位置参数 γ \gamma γ 。

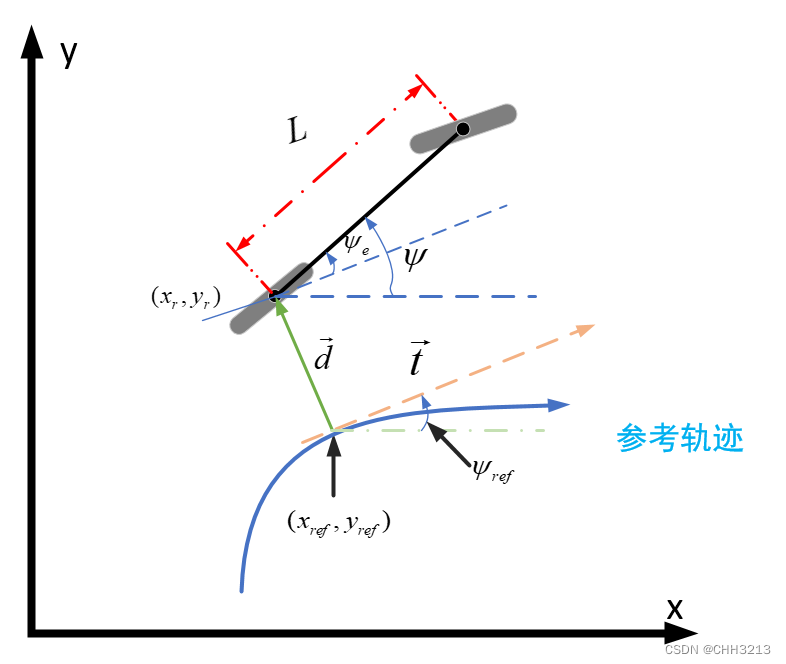
参考路径在 s ( t ) s(t) s(t) 参数处的单位切向量为 t ⃗ = ( ∂ x r e f ∂ s ∥ s ( t ) , ∂ y r e f ∂ s ∥ s ( t ) ) ∥ ( ∂ x r e f ( s ( t ) ) ∂ s , ∂ y r e f ( s ( t ) ) ∂ s ) ∥ = ( t x , t y ) (2) \tag{2} \vec{t}=\frac{\left(\frac{\partial x_{r e f}}{\partial s}\left\|_{s(t)}, \frac{\partial y_{r e f}}{\partial s}\right\|_{s(t)}\right)}{\left\|\left(\frac{\partial x_{r e f}(s(t))}{\partial s}, \frac{\partial y_{r e f}(s(t))}{\partial s}\right)\right\|}=\left(t_{x}, t_{y}\right) t =∥∥∥​(∂s∂xref​(s(t))​,∂s∂yref​(s(t))​)∥∥∥​(∂s∂xref​​∥∥∥​s(t)​,∂s∂yref​​∥∥∥​s(t)​)​=(tx​,ty​)(2) 跟踪误差向量表示如下: d ⃗ ( t ) = ( x r ( t ) − x r e f ( s ( t ) ) , y r ( t ) − y r e f ( s ( t ) ) ) = ( d x , d y ) (3) \tag{3} \vec{d}(t)=\left(x_{r}(t)-x_{r e f}(s(t)), y_{r}(t)-y_{r e f}(s(t))\right)=\left(d_{x}, d_{y}\right) d (t)=(xr​(t)−xref​(s(t)),yr​(t)−yref​(s(t)))=(dx​,dy​)(3) 所以跟踪误差向量 d ⃗ \vec{d} d 和参考路径上最近点的单位切向量 t ⃗ \vec{t} t 的叉积为 e ⃗ = t ⃗ × d ⃗ = ∣ t x t y d x d y ∣ = t x d y − t y d x (4) \tag{4} \vec{e}=\vec{t} \times \vec{d}=\left|\begin{array}{cc} t_{x} & t_{y} \\ d_{x} & d_{y} \end{array}\right|=t_{x} d_{y}-t_{y} d_{x} e =t ×d =∣∣∣∣​tx​dx​​ty​dy​​∣∣∣∣​=tx​dy​−ty​dx​(4)