以垃圾分类为例,神经网络的基本概念(tensorflow、keras)
- 一、概念简单
-
- 1.1 random
- 1.2 ImageDataGenerator()
- 1.3 flow
- 1.4 flow_from_directory
- 1.5 glob
- 1.6 enumerate()
- 1.7 fit_generator()
- 1.8 __getitem__
- 为什么使用激活函数
-
- 2.1 sigmoid
- 2.2 Tanh函数
- 2.3 ReLU
- softmax函数
- 如何选择激活函数?
- 三、CNN Tensorflow
-
- 3.1 卷积
- 3.2 池化
- 3.3 feature maps
- 四、LeNet5 卷积(经典手写数字识别)
-
- 4.1 调参
- 4.2 输入
- 4.3 C1层 (Conv1层)
- 4.4 S2层
- 4.5 C3层(Conv3层)
- 4.6 S4层
- 4.7 C5层(Conv5层)
- 4.8 F6层
- 4.9 OUTPUT层
- 4.10 卷积后输出维度的公式
- 五、CNN keras 垃圾分类代码
-
- 5.1 keras 基本概念
-
- 5.1.1 Sequential
- 5.1.2 指定输入数据的尺寸
- 5.1.3 编译
- 5.1.4 训练
- 垃圾分类实验
一、概念简单
1.1 random
''' random.random()函数是该模块中最常用的方法,它会产生一个随机的浮点,范围为0.0~1.0之间。 random.uniform()正好弥补了上述函数的不足,它可以设浮点数的范围,一个是上限,一个是下限。 random.randint()随机生一个整数int类型,可以指定整数的范围,也有上限和下限,python random.randint。 random.choice()可以从任何序列,例如list在列表中,选择可用于字符串、列表、元组等的随机元素返回。 random.shuffle()如果要随机打乱序列中的元素,可以使用此函数。 random.sample()指定长度的片段可以从指定的序列中随机截取,不需要原地修改。 ''' import random list = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] for i in range(3): slice = random.sample(list, 5) # 从list随机获取5个元素作为片段返回 print(slice) print(list, '\n') # 原始序列没有改变 ''' [3, 6, 2, 9, 10] [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] [9, 7, 1, 10, 5] [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] [1, 3, 8, 6, 10] [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] ''' 1.2 ImageDataGenerator()
ImageDataGenerator()是keras.preprocessing.image模块中的,同时也可以在batch增强数据,扩大数据集大小,增强模型的泛化能力。如旋转、变形、集成等。
keras.preprocessing.image.ImageDataGenerator(featurewise_center=False, samplewise_center=False, featurewise_std_normalization=False, samplewise_std_normalization=False, zca_whitening=False, zca_epsilon=1e-06, rotation_range=0.0, width_shift_range=0.0, height_shift_range=0.0, brightness_range=None, shear_range=0.0, zoom_range=0.0, channel_shift_range=0.0, fill_mode='nearest', cval=0.0, horizontal_flip=False, vertical_flip=False, rescale=None, preprocessing_function=None, data_format=None, validation_split=0.0)
-
featurewise_center: Boolean. 对输入的图片每个通道减去每个通道对应均值。
-
samplewise_center: Boolan. 每张图片减去样本均值, 使得每个样本均值为0。
-
featurewise_std_normalization(): Boolean()
-
samplewise_std_normalization(): Boolean()
-
zca_epsilon(): Default 12-6
-
zca_whitening: Boolean. 去除样本之间的相关性
-
rotation_range(): 旋转范围
-
width_shift_range(): 水平平移范围
-
height_shift_range(): 垂直平移范围
-
shear_range(): float, 透视变换的范围
-
zoom_range(): 缩放范围
-
fill_mode: 填充模式, constant, nearest, reflect
-
cval: fill_mode == 'constant’的时候填充值
-
horizontal_flip(): 水平反转
-
vertical_flip(): 垂直翻转
-
preprocessing_function(): user提供的处理函数
-
data_format(): channels_first或者channels_last
-
validation_split(): 多少数据用于验证集
1.3 flow
按batch_size大小从x,y生成增强数据
flow(x, y=None, batch_size=32, shuffle=True, sample_weight=None, seed=None, save_to_dir=None, save_prefix='', save_format='png', subset=None) ) ''' 接收numpy数组和标签为参数,生成经过数据提升或标准化后的batch数据,并在一个无限循环中不断的返回batch数据 x:样本数据,秩应为4.在黑白图像的情况下channel轴的值为1,在彩色图像情况下值为3 y:标签 batch_size:整数,默认32 shuffle:布尔值,是否随机打乱数据,默认为True save_to_dir:None或字符串,该参数能让你将提升后的图片保存起来,用以可视化 save_prefix:字符串,保存提升后图片时使用的前缀, 仅当设置了save_to_dir时生效 save_format:"png"或"jpeg"之一,指定保存图片的数据格式,默认"jpeg" yields:形如(x,y)的tuple,x是代表图像数据的numpy数组.y是代表标签的numpy数组.该迭代器无限循环. seed: 整数,随机数种子 '''
1.4 flow_from_directory
flow_from_directory()从路径生成增强数据,和flow方法相比最大的优点在于不用一次将所有的数据读入内存当中,这样减小内存压力,这样不会发生OOM,血的教训。 flow_from_directory()会从路径推测label, 在进行映射之前,会先对路径进行排序,具体顺序是alphanumerically, 也是os.listdir()对子目录排序的结果。这样你才知道具体来说哪个路径的类对应哪个label。
#flow_from_directory(directory): 以文件夹路径为参数,生成经过数据提升/归一化后的数据,在一个无限循环中无限产生batch数据
''' directory: 目标文件夹路径,对于每一个类,该文件夹都要包含一个子文件夹.子文件夹中任何JPG、PNG、BNP、PPM的图片都会被生成器使用.详情请查看此脚本 target_size: 整数tuple,默认为(256, 256). 图像将被resize成该尺寸 color_mode: 颜色模式,为"grayscale","rgb"之一,默认为"rgb".代表这些图片是否会被转换为单通道或三通道的图片. classes: 可选参数,为子文件夹的列表,如['dogs','cats']默认为None. 若未提供,则该类别列表将从directory下的子文件夹名称/结构自动推断。每一个子文件夹都会被认为是一个新的类。(类别的顺序将按照字母表顺序映射到标签值)。通过属性class_indices可获得文件夹名与类的序号的对应字典。 class_mode: "categorical", "binary", "sparse"或None之一. 默认为"categorical. 该参数决定了返回的标签数组的形式, "categorical"会返回2D的one-hot编码标签,"binary"返回1D的二值标签."sparse"返回1D的整数标签,如果为None则不返回任何标签, 生成器将仅仅生成batch数据, 这种情况在使用model.predict_generator()和model.evaluate_generator()等函数时会用到. batch_size: batch数据的大小,默认32 shuffle: 是否打乱数据,默认为True seed: 可选参数,打乱数据和进行变换时的随机数种子 save_to_dir: None或字符串,该参数能让你将提升后的图片保存起来,用以可视化 save_prefix:字符串,保存提升后图片时使用的前缀, 仅当设置了save_to_dir时生效 save_format:"png"或"jpeg"之一,指定保存图片的数据格式,默认"jpeg" flollow_links: 是否访问子文件夹中的软链接 '''
1.5 glob
import glob
#获取指定目录下的所有图片
print (glob.glob(r"/home/qiaoyunhao/*/*.png"),"\n")#加上r让字符串不转义
#获取上级目录的所有.py文件
1.6 enumerate()
函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列,同时列出数据和数据下标,一般用在 for 循环当中。
1.7 fit_generator()
&emsp使用fit_generator()分批训练,通过Python generator产生一批批的数据用于训练模型。generator可以和模型并行运行,例如,可以使用CPU生成批数据同时在GPU上训练模型。
fit_generator(self, generator,
steps_per_epoch=None,
epochs=1,
verbose=1,
callbacks=None,
validation_data=None,
validation_steps=None,
class_weight=None,
max_queue_size=10,
workers=1,
use_multiprocessing=False,
shuffle=True,
initial_epoch=0)
-
generator:一个generator或Sequence实例,为了避免在使用multiprocessing时直接复制数据。
-
steps_per_epoch:从generator产生的步骤的总数(样本批次总数)。通常情况下,应该等于数据集的样本数量除以批量的大小。
-
epochs:整数,在数据集上迭代的总数。
-
works:在使用基于进程的线程时,最多需要启动的进程数量。
-
use_multiprocessing:布尔值。当为True时,使用基于基于过程的线程。
1.8
这个方法返回与指定键想关联的值。对序列来说,键应该是0~n-1的整数,其中n为序列的长度。对映射来说,键可以是任何类型。
class Tag:
def __init__(self,id):
self.id=id
def __getitem__(self, item):
print('这个方法被调用')
return self.id
a=Tag('This is id')
print(a.id)
print(a['python'])
''' This is id 这个方法被调用 This is id '''
class Tag:
def __init__(self):
self.change = {
'python': 'This is python'}
def __getitem__(self, item):
print('这个方法被调用')
return self.change[item]
a = Tag()
print(a['python'])
''' 这个方法被调用 This is python '''
class Library(object):
def __init__(self):
self.books = ['title', 'a', 'title2', 'b', 'title3', 'c', ]
def __getitem__(self, i):
return self.books[i]
# def __iter__(self):
# 方法1 使用生成器
# for titles in self.books:
# yield self.books[titles]
# 方法2 使用迭代器
# return self.books.itervalues()
library = Library()
# 1.普通方法
print(library.books[1])
# 2.使用__getitem__
print(library[1])
# 3.迭代器
for book in library:
print(book)
''' a a title a title2 b title3 c '''
二、为什么用激活函数
输入的 inputs 通过加权,求和后,还被作用了一个函数,这个函数就是激活函数 Activation Function。 如果不用激励函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合。如果使用的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
2.1 sigmoid
sigmoid函数也叫 Logistic 函数,用于隐层神经元输出,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。 在特征相差比较复杂或是相差不是特别大时效果比较好。
- 激活函数计算量大,反向传播求误差梯度时,求导涉及除法
- 反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练
2.2 Tanh函数
也称为双切正切函数,取值范围为[-1,1]。 tanh在特征相差明显时的效果会很好,在循环过程中会不断扩大特征效果。 与 sigmoid 的区别是,tanh 是 0 均值的,因此实际应用中 tanh 会比 sigmoid 更好。
2.3 ReLU
Rectified Linear Unit(ReLU) - 用于隐层神经元输出;
输入信号 <0 时,输出都是0,>0 的情况下,输出等于输入
发现使用 ReLU 得到的 SGD 的收敛速度会比 sigmoid/tanh 快很多
训练的时候很”脆弱”,很容易就”die”了 例如,一个非常大的梯度流过一个 ReLU 神经元,更新过参数之后,这个神经元再也不会对任何数据有激活现象了,那么这个神经元的梯度就永远都会是 0. 如果 learning rate 很大,那么很有可能网络中的 40% 的神经元都”dead”了。
softmax函数
Softmax - 用于多分类神经网络输出; softmax是sigmoid的扩展,因为,当类别数 k=2 时,softmax 回归退化为 logistic 回归。具体地说,当 k=2 时,softmax 回归的假设函数为:
softmax建模使用的分布是多项式分布,而logistic则基于伯努利分布
多个logistic回归通过叠加也同样可以实现多分类的效果,但是 softmax回归进行的多分类,类与类之间是互斥的,即一个输入只能被归为一类;多个logistic回归进行多分类,输出的类别并不是互斥的,即"苹果"这个词语既属于"水果"类也属于"3C"类别。
激活函数的如何选择
如果使用 ReLU,要小心设置 learning rate,注意不要让网络出现很多 “dead” 神经元,如果不好解决,可以试试 Leaky ReLU、PReLU 或者 Maxout.
三、CNN + Tensorflow
3.1 卷积
简单来说对于给定的一幅图像来说,给定一个卷积核,卷积就是根据卷积窗口,进行像素的加权求和。 卷积神经网络与我们之前所学到的图像的卷积的区别,,一般来说,这个卷积核是已知的,比如各种边缘检测算子、高斯模糊等这些,都是已经知道卷积核,然后再与图像进行卷积运算。 然而神经网络卷积核是未知的,我们训练一个神经网络,就是要训练得出这些卷积核,而这些卷积核就相当于我们学单层感知器的时候的那些参数W,因此你可以把这些待学习的卷积核看成是神经网络的训练参数W。
import tensorflow as tf #定义一个卷积层 def conv2d(x,W): return tf.nn.conv2d(input, filter, strides, padding) ''' 1.使用TensorFlow定义一个卷积层时,需要使用的函数就是tf.nn.conv2d 该函数需要使用到四个参数: input:输入图像矩阵的shape为[批次大小,图像的高度,图像的宽度,图像的通道数], filter:卷积核,我们需要定义好卷积核的大小,通常是2 * 2,或2的倍数输入和输出都是单通道,通道数和个数。卷积核的shape为[卷积核的高度,卷积核的宽度,图像通道数,卷积核的个数], 因为我们不想在batch批次和channel通道上做池化,所以通常为1 strides:用来定义卷积核每次上下左右移动的步长,strides为[批次大小,高度方向的移动步长,宽度方向的移动步长,通道数] padding:决定此处卷积将采用哪种方式。 2.我在定义卷积层时采用函数的形式,conv2d函数需要传进来两个参数x,W, 分别对应input,和filter。值得注意的时,filter的维度要和input相对应才行。 例如我想对一组彩色图片进行卷积操作. 则假设x的维度为x=[10,128,128,3]。 在这里,x.shape[0]表示的时图片的个数,即十张。 x.shape[1]和x.shape[2]表示图片大小为128x128。 x.shape[3]表示图片的通道数,即3。 3.x维度确定好后,W(即filter)的维度也可以确定下来。 W=[5,5,3,16] 在这里,W.shape[0]和W.shape[1]表示的卷积核的大小为5x5。 W.shape[2]表示卷积核的通道数,一定要注意,在定义卷积核通道数时,要和输入的图片的通道数相一致才行,既输入图片通道数为m,则卷积核的通道数也要为m x.shape[3]表示卷积核的个数,既16。每次卷积有多少个卷积核,则经过卷积后输出的图片通道数就有多少。 4.关于参数strides strides=[a,b,c,d]这四个变量中,a和d一般情况下都设置为1。 b,c分别表示在卷积时,卷积核每次左右移动步长为b,上下移动步长为c 一般定义是strides=[1,1,1,1] 5.关于参数padding 在卷积里面padding的方式有两种,为"SAME"和”VALID" 使用SAME时,经过卷积后输出的图片大小和输入的大小一致。 使用VALID时,经过卷积后输出的图片大小会小于输入的图片大小,而输出的图片大小具体为多少,可以根据我上面提供的公式进行计算。 '''
3.2 池化
所谓的池化,就是图片下采样。CNN每一层的构建跟图像高斯金字塔的构建有点类似,在高斯金子塔构建中,每一层通过卷积,然后卷积后进行下采样,而CNN也是同样的过程。 CNN的池化(图像下采样)方法很多:Mean pooling(均值采样)、Max pooling(最大值采样)、Overlapping (重叠采样)、L2 pooling(均方采样)、Local Contrast Normalization(归一化采样)、Stochasticpooling(随即采样)、Def-pooling(形变约束采样)。其中最经典的是最大池化。
import tensorflow as tf
#最大池化层
def max_pool_2x2(x):
return tf.nn.max_pool(value, ksize, strides, padding)
""" 1.在使用TensorFlow实现池化是,我选择用tf.nn.max_pool这个函数,最大池化。 最大池化就是在池化窗口中,选取里面最大值出来。把其他值给舍去。tf.nn.max_pool这个函数 也一样需要四个参数,分别为value,ksize,strides,padding。 value:需要进行池化的输入。 ksize:池化窗口,是一个四维向量。 strides:进行池化时,池化窗口上下左右移动的步长。 padding:和卷积类型,决定池化的方式。 2.我在定义定义池化层的时候也同样采用了函数的形式,max_pool_2x2(x) x很明显就是需要进行池化的输入,应该放在参数value的位置。 假设我想对一组彩色图片进行池化操作。图片数量为10. 则x=[10,128,128,3]. 在这里,x.shape[0]表示的时图片的个数,即十张。 x.shape[1]和x.shape[2]表示图片大小为128x128。 x.shape[3]表示图片的通道数,即3。 3.ksize 上面说了,ksize是一个思维向量。 ksize=[a,h,w,b] a和b分别表示batch和channel,因为一般情况下我们不在batch和channel上面进行池化操作,所以a和b的值一般设为1。h和w就是池化窗口的大小了。 4.strides 同卷积一样 strides=[a,b,c,d]这四个变量中,a和d一般情况下都设置为1。 b,c分别表示在卷积时,卷积核每次左右移动步长为b,上下移动步长为c 一般定义是strides=[1,1,1,1] 5.关于参数padding 在池化里面padding的方式有两种,为"SAME"和”VALID" 具体含义见下图所示。 """
3.3 feature maps
feature map:是输入图像和卷积核卷积后生成的feature map,图像的特征。如果是灰度图片,那就只有一个feature map;如果是彩色图片(RGB),一般就是3个feature map(红绿蓝),层与层之间会有若干个卷积核(kernel),上一层和每个feature map跟每个卷积核做卷积,都会产生下一层的一个feature map。 feature maps也叫特征图,特征图其实说白了就是CNN中的每张图片,都可以称之为特征图张。在CNN中,我们要训练的卷积核并不是仅仅只有一个,这些卷积核用于提取特征,卷积核个数越多,提取的特征越多,理论上来说精度也会更高,然而卷积核一堆,意味着我们要训练的参数的个数越多。在LeNet-5经典结构中,第一层卷积核选择了6个,而在AlexNet中,第一层卷积核就选择了96个,具体多少个合适,还有待学习。 CNN的每一个卷积层我们都要人为的选取合适的卷积核个数,及卷积核大小。每个卷积核与图片进行卷积,就可以得到一张特征图了,比如LeNet-5经典结构中,第一层卷积核选择了6个,我们可以得到6个特征图,这些特征图也就是下一层网络的输入了。我们也可以把输入图片看成一张特征图,作为第一层网络的输入。
四、LeNet5 卷积(经典手写数字识别)
4.1 调参
在现实使用中,每一层特征图需要多少个,卷积核大小选择,还有池化的时候采样率要多少,等这些都是变化的,这就是所谓的CNN调参,我们需要学会灵活多变。
4.2 输入
读入需要被网络处理的图片,这里图片的大小为32*32的黑白图片,这些手写字体包含0~9数字,也就是相当于10个类别的图片
4.3 C1层 (Conv1层)
6个5 * 5特征卷积核,步长是1,采用的卷积方式是vaild,然后得到6个特征图,每个特征图的大小为32-5+1=28,输出:28x28x6,也就是神经元的个数为6 * 28 * 28=784。 C1层是卷积层,单通道下用了6个卷积核,这样就得到了6个feature map,其中每个卷积核的大小为5 * 5,用每个卷积核与原始的输入图像进行卷积,这样feature map的大小为(32-5+1)×(32-5+1)= 28×28,所需要的参数的个数为(5×5+1)×6= 156(其中5×5为卷积模板参数,1为偏置参数),连接数为(5×5+1)×28×28×6=122304(其中28×28为卷积后图像的大小)。
4.4 S2层
这就是下采样层,也就是使用最大池化进行下采样,池化的size,选择(2,2),也就是相当于对C1层28 * 28的图片,进行分块,每个块的大小为2 * 2,这样我们可以得到14 * 14个块,然后我们统计每个块中,最大的值作为下采样的新像素,因此我们可以得到S2结果为:6个14 * 14大小的图片。 S2层为 pooling 层,也可以说是池化或者特征映射的过程,拥有6个 feature map,每个feature map的大小为14 * 14,每个feature map的隐单元与上一层C1相对应的feature map的 2×2 单元相连接,这里没有重叠。计算过程是:2×2 单元里的值相加然后再乘以训练参数w,再加上一个偏置参数b(每一个feature map共享相同w和b),然后取sigmoid (S函数:0-1区间)值,作为对应的该单元的值。所以S2层中每 feature map 的长宽都是上一层C1的一半。S2层需要2×6=12个参数,连接数为(4+1)×14×14×6 = 5880。下面为卷积操作与池化的示意图:
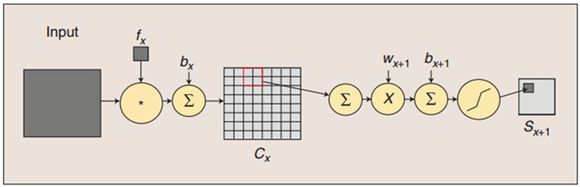
4.5 C3层(Conv3层)
C3卷积层,我们选择卷积核的大小依旧为5 * 5,据此我们可以得到新的图片大小为14-5+1=10,然后我们图。我们知道S2包含:6张14 * 14大小的图片,我们希望这一层得到的结果是:16张10 * 10的图片。这16张图片的每一张,是通过S2的6张图片进行加权组合得到的,具体是怎么组合的呢? C3层也是一个卷积层(多通道(14个通道)),16核卷积,注意此处,见下图),有16个卷积核,卷积模板的大小为5 * 5,因此具有16个feature maps,每个feature map的大小为(14-5+1)×(14-5+1)= 10×10。每个feature map只与上一层S2中部分feature maps相连接,下表给出了16个feature maps与上一层S2的连接方式(行为S2层feature map的标号,列为C3层feature map的标号,第一列表示C3层的第0个feature map只有S2层的第0、1和2这三个feature maps相连接,其它解释类似)。为什么要采用部分连接,而不采用全连接呢?首先就是部分连接,可计算的参数就会比较少,其次更重要的是它能打破对称性,这样就能得到输入的不同特征集合。以第0个feature map描述计算过程:用1个卷积核(对应3个卷积模板,但仍称为一个卷积核,可以认为是三维卷积核)分别与S2层的3个feature maps进行卷积,然后将卷积的结果相加,再加上一个偏置,再取sigmoid就可以得出对应的feature map了。所需要的参数数目为(5×5×3+1)×6 +(5×5×4+1)×9 +5×5×6+1 = 1516(5×5为卷积参数,卷积核分别有 3 4 6 个卷积模板),连接数为1516 * 10 * 10= 151600 (98论文年论文给出的结果是156000,个人认为这是错误的,因为一个卷积核只有一个偏置参数 ?)。
4.6 S4层
下采样层,对C3的16张10 * 10的图片进行最大池化,池化块的大小为2 * 2。因此最后S4层为16张大小为5 * 5的图片。至此我们的神经元个数已经减少为:16 * 5 * 5=400。 S4层也是采样层,有16个feature maps,每个feature map的大小为5×5,计算过程和S2类似,需要参数个数为16×2 = 32个,连接数为(4+1)×5×5×16 = 2000.
4.7 C5层(Conv5层)
我们继续用5 * 5的卷积核进行卷积,采用的卷积方式:vaild,。这样C5层图片的大小为5-5+1=1,也就是相当于1个神经元,120个特征图,因此最后只剩下120个神经元了。这个时候,神经元的个数已经够少的了,后面我们就可以直接利用全连接神经网络,进行这120个神经元的后续处理。 C5为卷积层,有120个卷积核,卷积核的大小仍然为5×5,因此有120个feature maps,每个feature map的大小都与上一层S4的所有feature maps进行连接,这样一个卷积核就有16个卷积模板。Feature map的大小为1×1,这样刚好变成了全连接,但是我们不把它写成F5,因为这只是巧合。C5层有120 * (5 * 5 * 16+1) = 48120(16为上一层所有的feature maps个数)参数(自己的理解:和 C3的不同,这一层一共有120个16维的5 * 5大小的卷积核,且每一个核中的16维模板都一样),连接数也是这么多。
4.8 F6层
输入向量维度:[1,120] 权重参数的维度:[120,86] 计算方式:输入的向量与权重参数之间用矩阵点积的方式进行运算,得到一个输出维度为[1,86]的向量 F6层有86个神经单元,每个神经单元与C5进行全连接。它的连接数和参数均为 86 × 120 = 10164 。这样F6层就可以得到一个86维特征了。后面可以使用该86维特征进行做分类预测等内容了。注意:这里卷积和池化的计算过程和ufldl教程中的计算略有不同。
4.9 OUTPUT层
输入向量维度:[1,86]
权重参数的维度:[86,10]
计算方式:输入的向量与权重参数之间用矩阵点积的方式进行运算,得到一个输出维度为[1,10]的向量
4.10 附经过卷积后输出维度大小的公式
N: 输入的维度、F:卷积核大小、stride: 步长、pad: 扩充边缘
''' 输入数据维度为W*W Filter大小 F×F 步长 S padding的像素数 P 可以得出:N = (W − F + 2P )/S+1 输出大小为 N×N Valid卷积意味着不填充,这样的话,如果你有一个n×n的图像, 用一个f×f的过滤器卷积,它将会给你一个(n-f+1)×(n-f+1)维的输出。 Same卷积,那意味你填充后,你的输出大小和输入大小是一样的。根据这个公式n-f+1, 当你填充p个像素点,n就变成了n+2p,最后公式变为n+2p-f+1。因此如果你有一个n×n的图像, 用p个像素填充边缘,输出的大小就是这样的(n+2p-f+1)×(n+2p-f+1)。如果你想让n+2p-f+1=n的话, 使得输出和输入大小相等,如果你用这个等式求解p,那么p=(f-1)/2。所以当f是一个奇数的时候, 只要选择相应的填充尺寸,你就能确保得到和输入相同尺寸的输出。 '''
五、CNN + keras 垃圾分类代码
5.1 keras 基本概念
https://keras.io/zh/models/sequential/
5.1.1 Sequential
Keras实现了很多层,包括core核心层,Convolution卷积层、Pooling池化层等非常丰富有趣的网络结构。我们可以通过将层的列表传递给Sequential的构造函数,来创建一个Sequential模型。
from keras.models import Sequential
from keras.layers import Dense, Activation
model = Sequential([
Dense(32, input_shape=(784,)),
Activation('relu'),
Dense(10),
Activation('softmax'),
])
model = Sequential()
model.add(Dense(32, input_dim=784))
model.add(Activation('relu'))
5.1.2 指定输入数据的尺寸
模型需要知道它所期待的输入的尺寸(shape)。出于这个原因,序贯模型中的第一层(只有第一层,因为下面的层可以自动的推断尺寸)需要接收关于其输入尺寸的信息,后面的各个层则可以自动的推导出中间数据的shape,因此不需要为每个层都指定这个参数。有以下几种方法来做到这一点:
- 传递一个input_shape参数给第一层。它是一个表示尺寸的元组(一个整数或None的元组,其中None表示可能为任何正整数)。3 通道 100x100 像素图像 -> (100, 100, 3) 张量。使用 32 个大小为 3x3 的卷积滤波器。model.add(Conv2D(32, (3, 3), activation=‘relu’, input_shape=(100, 100, 3))),在input_shape中不包含数据的batch大小。
- 某些 2D 层,例如 Dense,支持通过参数 input_dim 指定输入尺寸,某些 3D 时序层支持 input_dim 和 input_length 参数。卷积层Conv2D:二维卷积层,即对图像的空域卷积。该层对二维输入进行滑动窗卷积,当使用该层作为第一层时,应提供input_shape参数。例如input_shape = (128,128,3)代表128*128的彩色RGB图像
- 如果你需要为你的输入指定一个固定的 batch 大小(这对 stateful RNNs 很有用),你可以传递一个 batch_size 参数给一个层。如果你同时将 batch_size=32 和 input_shape=(6, 8) 传递给一个层,那么每一批输入的尺寸就为 (32,6,8)。
model = Sequential()
model.add(Dense(32, input_shape=(784,)))
# 或者
model = Sequential()
model.add(Dense(32, input_dim=784))
# 下面三种方法也是严格等价的
model = Sequential()
model.add(LSTM(32, input_shape=(10, 64)))
# 或者
model = Sequential()
model.add(LSTM(32, batch_input_shape=(None, 10, 64)))
# 或者
model = Sequential()
model.add(LSTM(32, input_length=10, input_dim=64))
5.1.3 编译
compile(optimizer, loss=None, metrics=None, loss_weights=None, sample_weight_mode=None, weighted_metrics=None, target_tensors=None)
在训练模型之前,我们需要配置学习过程,这是通过compile方法完成的,他接收三个参数:
- 优化器 optimizer:它可以是现有优化器的字符串标识符,如 rmsprop 或 adagrad,也可以是 Optimizer 类的实例。详见:optimizers。
- 损失函数 loss:模型试图最小化的目标函数。它可以是现有损失函数的字符串标识符,如 categorical_crossentropy 或 mse,也可以是一个目标函数。详见:losses。
- 评估标准 metrics:对于任何分类问题,你都希望将其设置为 metrics = [‘accuracy’]。评估标准可以是现有的标准的字符串标识符,也可以是自定义的评估标准函数。
# 多分类问题
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
# 二分类问题
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
# 均方误差回归问题
model.compile(optimizer='rmsprop',
loss='mse')
# 自定义评估标准函数
import keras.backend as K
def mean_pred(y_true, y_pred):
return K.mean(y_pred)
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy', mean_pred])
5.1.4 训练
Keras 模型在输入数据和标签的 Numpy 矩阵上进行训练。为了训练一个模型,你通常会使用 fit 函数。
# 对于具有2个类的单输入模型(二进制分类): model = Sequential() model.add(Dense(32, activation='relu', input_dim=100)) model.add(Dense(1, activation='sigmoid')) model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['accuracy']) # 生成虚拟数据 import numpy as np data = np.random.random((1000, 100 标签:mse压力变送器