【通信】【1】幅度调制，频率调制，双边带与单边带，IQ与PSK与QAM——采样一定要满足奈奎斯特定理吗

见过宽带太赫兹通信IQ，BPSK等词汇，想想我学到的没有印象的通信原理，是时候弥补了。通信原理 简单易懂的写作太好了。为什么去年学了几天就放弃了一两个小时就能学会的频带信号发送和接收第七章？因为我总是想弥补通信原理的基础，从头开始，但我不太懂知识，这让人很困惑。此外，当时压力不大，我放弃了。

?? ?? ?? \;\\\;\\\;

当信号（低频）大于零时，可以直接混频，乘上载波信号(高频)。但是信号一般小于零，所以调整幅度是在混频之前提高信号幅度。

s ( t ) = ( f ( t ) A 0 ) ? c o s ω c t s(t) = ( f(t) A_0 ) \cdot cos \omega_c t s(t)=(f(t) A0)?cosωct 其中 f ( t ) f(t) f(t)是信号， A 0 A_0 A0​是提高的电平

   \;

解调通过三个步骤

1. 利用二极管单向导通，去掉负数部分
2. 低频滤波，去掉高频的载波，只留下低频信号（ s ( t ) s(t) s(t)的包络）
3. 利用电容隔直通交，将基带信号搬移回零电平附近？

         \;\\\;\\\;

s ( t ) = ( f ( t ) + A 0 ) ⋅ c o s ω c t = f ( t ) c o s ω c t + A 0 c o s ω c t s(t)= ( f(t) + A_0 ) \cdot cos \omega_c t = f(t) cos \omega_c t + A_0 cos \omega_c t \quad s(t)=(f(t)+A0​)⋅cosωc​t=f(t)cosωc​t+A0​cosωc​t 后面一项没有承载信息

幅度调制效率低，电平 A 0 > ∣ f ( t ) ∣ A_0>|f(t)| A0​>∣f(t)∣，调制效率低于50%

         \;\\\;\\\;

调制： s ( t ) = f ( t ) ⋅ c o s ω c t 调制：s(t)=f(t) \cdot cos \omega _c t 调制：s(t)=f(t)⋅cosωc​t 相干解调： s ( t ) ⋅ c o s ω c t ⇒ L P F ⇒ f ( t ) f ( t ) ⋅ c o s ω c t ⋅ c o s ω c t = 1 2 f ( t ) + 1 2 c o s 2 ω c t 相干解调：s(t) \cdot cos \omega_c t \Rightarrow LPF \Rightarrow f(t) \\\\ f(t) \cdot cos \omega _c t \cdot cos \omega _ct = \frac{1}{2}f(t) + \frac{1}{2} cos 2 \omega _ct 相干解调：s(t)⋅cosωc​t⇒LPF⇒f(t)f(t)⋅cosωc​t⋅cosωc​t=21​f(t)+21​cos2ωc​t

相干解调：在接收端同步信息，产生一个与高频载波同频同相的本地载波，再与接收信号混频…

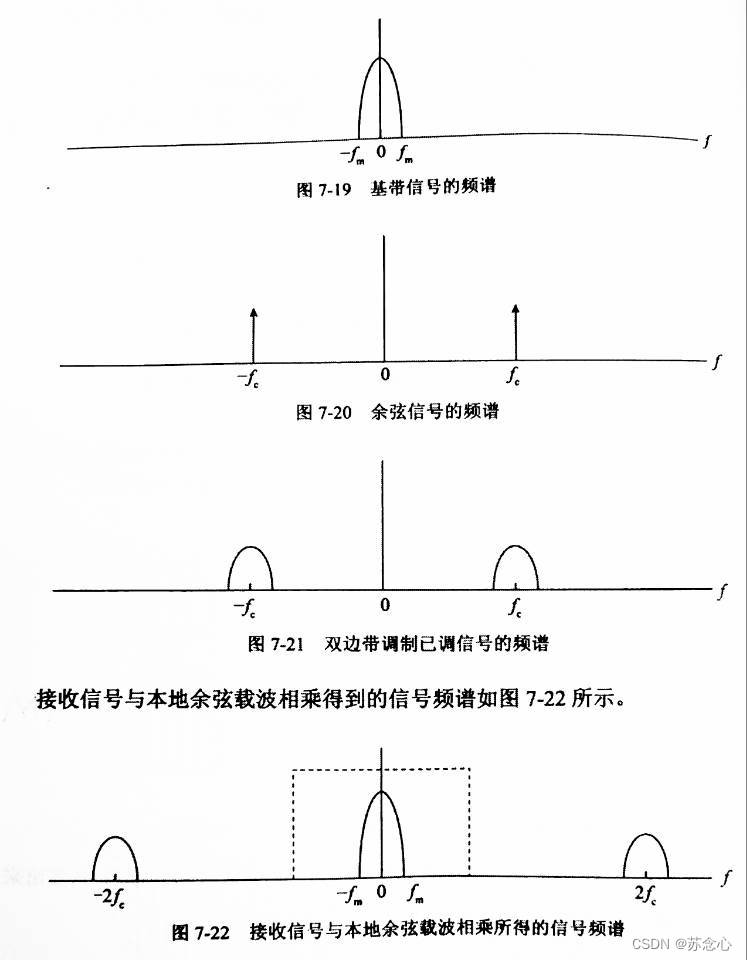
在双边带已调信号的频谱（第三个图）中， ∣ f ∣ < f c |f|<f_c ∣f∣<fc​ 的部分是下边带， ∣ f ∣ > f c |f|>f_c ∣f∣>fc​ 的部分是上边带。

• 两个上边带，分别是基带信号的频谱的左右部分左移和右移形成的

• 左边的下边带，是基带信号的频谱的右边左移形成的

• 右边的下边带，是基带信号的频谱的左边右移形成的

上边带携带的信息 = 下边带携带的信息 上边带携带的信息 = 下边带携带的信息 上边带携带的信息=下边带携带的信息

所以只需要上边带或者下边带就行了!

         \;\\\;\\\;

调制： S D S B ( t ) = f ( t ) ⋅ c o s ω c t 调制：S_{DSB}(t) = f(t)\cdot cos \omega _c t 调制：SDSB​(t)=f(t)⋅cosωc​t 相干解调： s ( t ) ⋅ c o s ω c t ⇒ L P F ⇒ f ( t ) f ( t ) ⋅ c o s ω c t ⋅ c o s ω c t = 1 2 f ( t ) + 1 2 c o s 2 ω c t 相干解调：s(t) \cdot cos \omega_c t \Rightarrow LPF \Rightarrow f(t) \\\\ f(t) \cdot cos \omega _c t \cdot cos \omega _ct = \frac{1}{2}f(t) + \frac{1}{2} cos 2 \omega _ct 相干解调：s(t)⋅cosωc​t⇒LPF⇒f(t)f(t)⋅cosωc​t⋅cosωc​t=21​f(t)+21​cos2ωc​t

采用两路载波，

1. c o s ω c t cos \omega_c t cosωc​t
2. − s i n ω c t -sin \omega _ct −sinωc​t

同理，也同时输出两路信号 s ( t ) c o s ω c t = 1 2 x ( t ) + 1 2 x ( t ) c o s 2 ω c t − 1 2 y ( t ) s i n 2 ω c t s(t) cos \omega _ct = \frac{1}{2}x(t) + \frac{1}{2} x(t) cos 2\omega _ct - \frac{1}{2} y(t) sin 2\omega _c t s(t)cosωc​t=21​x(t)+21​x(t)cos2ωc​t−21​y(t)sin2ωc​t − s ( t ) s i n ω c t = 1 2 y ( t ) − 1 2 x ( t ) s i n 2 ω c t − 1 2 y ( t ) c o s 2 ω c t -s(t)sin\omega _ct = \frac{1}{2}y(t) - \frac{1}{2} x(t) sin 2\omega _ct - \frac{1}{2} y(t) cos 2\omega _c t −s(t)sinωc​t=21​y(t)−21​x(t)sin2ωc​t−21​y(t)cos2ωc​t

         \;\\\;\\\;

二相移键控

0 0 0 对应 载波相位为 0 0 0， f ( t ) = c o s ω c t f(t) = cos \omega _c t f(t)=cosωc​t

1 1 1 对应 载波相位为 π \pi