资讯详情

unity3D数学基础-坐标系、向量、矩阵

坐标系

左右手坐标系

  1. ：伸开左手，拇指指向X轴，食指指向Y轴，其他三个指向Z轴。
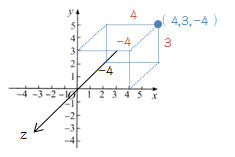
  2. ：伸开右手，拇指指向X轴，食指指向Y轴，其他三个指向Z轴。 请添加图片描述

3D笛卡尔坐标系：右手坐标系 OpenGL：右手坐标系 Direct3D：左手坐标系 Unity3D：左手坐标系(世界坐标系)，即 x, y, z指向右边，上面和前面。

各种坐标空间(坐标系)

部分空间类型

  • unity约定：左手坐标系，XYZ对应右上前。
  • 艺术家通常在建模软件中确定模型空间的原点和坐标轴。当导入时unity在顶点着色器中，我们可以访问模型的顶点信息，包括每个顶点的坐标，它们是由模型空间中的原点（通常位于模型的重心）定义的。
  • 视图中显示的是localPosition的值。
  • transform.localPosition(本地坐标)可获得父物局部坐标系中物体的位置点。
  • unity协议：使用左手坐标系，但它XYZ轴是固定的。
  • transform.position获取游戏对象的世界坐标。
  • 目标是方便地切割渲染元：完全位于空间内的元将被保留，完全位于空间外的元将被删除，与空间边界相交的元将被切割。
  • 这个空间由视椎体决定。
  • 左手坐标系
  • 屏幕的左下角为(0，0)，右上角为（Screen.width, Screen.height），z轴坐标是相机世界坐标中z轴坐标的负值。
  • 屏幕空间是二维空间。
  • 鼠标位置坐标属于屏幕坐标，通过Input.mousePosition位置坐标可以获得。
  • 手指触摸屏幕也是屏幕坐标，Input.GetTouch(0).position当单个手指触摸屏幕时，可以获得手指的坐标。
  • 将Game视图屏幕坐标系单位化
  • 左下角(0，0)，右上角(1，1)。z轴坐标是相机世界坐标中z轴坐标的负值。

相互空间转换

  • 模型变换：顶点转换的第一步是将顶点从模型空间转换为世界空间。这种转换通常被称为模型转换。请注意，这里的转换顺序不能交换，即先缩放，然后旋转，最后平移，然后我们可以构建模型转换的转换矩阵（因为矩阵不符合交换定律，所以不要随意更换转换顺序）
  • 观察变换：顶点变换的第二步，就是将顶点坐标从世界空间变换到观察空间中，这个变换通常叫做观察变换。一种方法是计算世界空间下观察空间中三个坐标轴的表示，然后构建从世界空间到观察空间的转换矩阵。另一种方法是想象平移整个观察空间，让相机的原点位于世界坐标的原点，坐标轴与世界空间中的坐标轴重叠
  • 投影变换：顶点转换的第三步是将顶点坐标从观察空间转换为切割空间（也称为齐次切割空间）。这种转换通常称为投影转换，用于转换的矩阵称为切割矩阵，也称为投影矩阵。
    • 目的：首先是为投影做准备。真正的投影发生在后续的齐次除法过程中。投影矩阵变换后，顶点的w重量具有特殊意义；其次是x,y,z重量缩放。
    • 视椎体指的是空间中的一块区域，这块区域决定了摄像机可以看到的空间。视椎体由两种类型，这涉及两种投影：一种是正交投影，一种是透视投影。
    • 投影：可以理解为空间的维度降低，如从四维空间投影到三维空间，投影矩阵实际上并不是真正的投影，它将为真正的投影做准备。真正的投影将发生在屏幕映射中，并通过齐次除法获得二维坐标。
  • 屏幕映射：将顶点从裁剪空间投影到屏幕空间，生成相应的2D坐标。在unity在中间，从切割空间到屏幕空间的转换通常是由底层完成的，我们的顶点着色器只需要将顶点转换为切割空间。最后，通过齐次除法和映射到屏幕上。——分为两个步骤：一是标准齐次除法，又称透视除法。用齐次坐标系的w分量去除x，y，z重量；透视投影和正交投影的视椎体在齐次除法后变成同一立方体。接下来可以根据 变换后的x和y坐标映射输出窗口对应的像素坐标。
  • Transform.forward, Transform.right, Transform.up：目前物体坐标系的z轴，x轴，y轴指向世界坐标系。
  • Transform.TransformPoint(Vector3 position) :将坐标点从局部坐标系转换为全局坐标系。
  • Transform.InverseTransformPoint(Vector3 position)：将坐标点从全局坐标系转换为局部坐标系。
  • Transform.TransformDirection(Vector3 direction):将一个方向从局部坐标系转变为全局坐标系。
  • Transform.InverseTransformDirection(Vector3 direction)：将一个方向从全局坐标系转换到局部坐标系。
  • Transform.TransformVector(Vector3 vector):将向量从局部坐标系转换为全局坐标系。
  • Transform.InverseTransformVector(Vector3 vector):将向量从全局坐标系转换为局部坐标系。
  • Camera.ScreenToWorldPoint(Vector3 position): 将屏幕坐标转换为全局坐标。
  • Camera.WorldToScreenPoint(Vector3 position):将全局坐标转换为屏幕坐标。
  • Camera.ScreenToViewportPoint(Vector3 position)：将屏幕坐标转换为视口坐标。
  • Camera.ViewportToScreenPoint(Vector3 position)：将视觉坐标转换为屏幕坐标。
  • Camera.WorldToViewportPoint(Vector3 position)：将全局坐标转换为视口坐标。
  • Camera.ViewportToWorldPoint(Vector3 position)：将视口坐标转换为全局坐标。

向量

认识向量

  • 在数学中，向量（也称为矢量），是指具有大小和方向的量；书写向量时，水平书写的向量叫做行向量 [ 1 2 3 ] \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} [1​2​3​] 垂直书写的向量叫做列向量。 [ 1 2 3 ] \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} ⎣⎡​123​⎦⎤​
  • 向量的大小就是向量的长度，也叫做模。向量的方向描述了空间中向量的指向；向量中的数表达了向量在每个维度上的有向位移。
  • 点中的数表示了一个位置，它没有大小、方向的概念；点只有位置，适量只有方向和大小，任何一个点都可以表示成一个从原点出发的矢量。

向量运算

特殊向量

  1. 零向量：大小为0，没有方向的向量，并且它不可以被归一化。
  2. 负向量：向量变负,将得到一个和原向量方向相反、大小相等的向量。
  3. 单位向量：也叫做标准化向量，就是大小为1的向量；对任意的非零向量，我们都可以计算出它的单位向量，即将其归一化(normalization)。单位向量的表示 a ^ = a ∣ a ∣ \widehat{\bf{a}} =\frac{\bf{a}}{\begin{vmatrix} \bf{a} \end{vmatrix}} a =∣∣​a​∣∣​a​
  4. 在Unity中，可以使用Vector3.Normalize来归一化向量。使用Vector3.normalized来获得归一化后的单位向量；Vector3.Normalize改变当前向量，Vector3.normalized当前向量是不改变的并且返回一个新的规范化的向量。

向量的长度

  1. 即向量的大小，或者向量的模。
  2. 向量的大小就是向量各分量平方和的平方根
  3. 在Unity中，可以通过Vector3.magnitude计算向量的长度。Vector3.sqrMagnitude则返回向量长度的平方；Vector3.Distance(A,B)可以计算2个点A,B之间的距离，即返回向量AB或向量BA的长度。

向量与标量的乘/除法

  1. 向量与标量的乘法，即将向量的每个分量分别与标量相乘。
  2. 向量与非零标量的除法，即乘以该标量的倒数。

向量的加/减法

  1. 只有在两个向量的维度相同时，才可以相加或相减。
  2. 向量的加法和减法，即将向量的各个分量相加或相减。
  3. 向量的加法满足交换律和结合律，向量的减法仅满足结合律。
  4. 几何意义：对于加法，我们可以把矢量a的头连接到矢量b的尾，然后画一条从a的尾到b的头的矢量，来得到a和b相加后的矢量。减法类似
  5. 公式： a ⃗ + b ⃗ = ( a x + b x , a y + b y , a z + b z ) a ⃗ − b ⃗ = ( a x − b x , a y − b y , a z − b z ) \vec{a} + \vec{b}=(a_x+b_x,a_y+b_y,a_z+b_z) \\ \vec{a} - \vec{b}=(a_x-b_x,a_y-b_y,a_z-b_z) a +b =(ax​+bx​,ay​+by​,az​+bz​)a −b =(ax​−bx​,ay​−by​,az​−bz​)

向量的点积

  1. 也叫做向量的内积。表示如下：其中点不可以省略 a ⃗ ⋅ b ⃗ \vec{a} \cdot \vec{b} a ⋅b
  2. 两种计算公式如下： a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ cos ⁡ θ a ⃗ ⋅ b ⃗ = ( a x b x + a y b y + a z b z ) \vec{a} \cdot \vec{b}=\rvert \vec{a} \rvert \rvert \vec{b} \rvert \cos \theta \\ \vec{a} \cdot \vec{b}=(a_xb_x+a_yb_y+a_zb_z) a ⋅b =∣a ∣∣b ∣cosθa ⋅b =(ax​bx​+ay​by​+az​bz​)
  3. 点积满足交换律。
  4. 向量点积的结果是一个标量
  5. 几何意义：
    • 点乘结果描述了两个向量的“相似”程度，点乘结果越大，两向量越相近
    • 投影：向量在向量上的投影的长度可以表示为 ∣ b ⃗ → a ⃗ ∣ = ∣ b ⃗ ∣ cos ⁡ θ = a ⃗ ⋅ b ⃗ ∣ a ⃗ ∣ \begin{vmatrix} \vec{b} \to \vec{a} \end{vmatrix}=\begin{vmatrix} \vec{b} \end{vmatrix} \cos \theta=\frac{\vec{a} \cdot \vec{b}}{\begin{vmatrix} \vec{a} \end{vmatrix}} ∣∣∣​b →a ​∣∣∣​=∣∣∣​b ​∣∣∣​cosθ=∣∣​a ​∣∣

标签： t型m12连接器m12连接器孔型

锐单商城拥有海量元器件数据手册、 IC替代型号，打造 电子元器件IC百科大全！

锐单商城 - 一站式电子元器件采购平台