继续往后学习,逻辑代数基础,从上一章的图可以看出,逻辑代数是学习数字逻辑设计的基础。
第2章 逻辑代数基础
本节来说三种基本逻辑运算,与或非,分别从逻辑表达式、真值表、逻辑符号和典型芯片来说。
2.1 基本逻辑操作
2.1.1 AND(逻辑与)
逻辑与概念
逻辑乘又称逻辑乘,F=A*B,只有当A和B同时为1时,F=1;否则,F=0.逻辑与相当于电路的串联,从电路图中可以看出,只有A和B同时为1时,F灯亮了。下图右侧是相应的真值表。 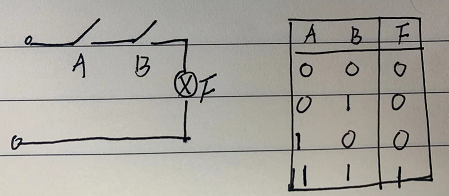
逻辑符号
以下符号表示逻辑符号。
典型芯片:74LS08
芯片由四个逻辑组成,7号引脚接地,表示低电平;14号引脚表示高电平。只有A和B高电平时输入信号,F才有效。
2.1.2 OR (逻辑或)
逻辑或概念
逻辑也叫逻辑加,F = A B,相当于电路并联,真值表如下图所示。
逻辑或符号
典型芯片7432
下图左侧是典型的芯片,由四个或门组成;右边是A和B当A和B一个高电平时,F输出高电平。
2.1.3 !(逻辑非)
逻辑非概念
逻辑非也叫反相器,F=A;逻辑相当于开关并联小灯,当A关闭时,小灯熄灭;当A断开时,小灯亮起。相应的真值表如下图所示。
逻辑非逻辑符号
非典型的逻辑芯片
如左图所示,典型芯片由六个非门组成;右图中,当A输入高电平时,F输出为低电平;相反,F输出低电平。
2.2 复合逻辑操作
如下图所示,共有五种类型。
2.2.1 与非(NAND)
2.2.2 或非(NOR)
2.2.3 与或非
2.2.4 异或
2.2.5 同或
2.3 表示逻辑函数的方法
关系如下:
2.3.1 逻辑图和逻辑表达式的转换
2.3.2 转换真值表和逻辑表达式
这两种逻辑表达式是如何相等的?
2.4 逻辑代数定理及规则
2.4.1 公理
略
2.4.2 基本定理
0-1律、互补率、重叠率、分配率(重点)
对偶定理(重点)德摩根定理
去冗余项
2.5 代数化简
代数化简的目的是节约门的数量,从而减少成本。 给出两个例子,运用前边的公式(摩根,对偶),把公式化成最简。