前边介绍了TensorFlow神经网络的基本操作和大量知识:
tf2.学习(1)-基础知识 tf2.学习(2)-高级知识 tf2.0学习(3)-神经网络 tf2.学习(4)-反向传播算法 tf2.0学习(五)——Keras高层接口 以下是强化学习的介绍:
tf2.学习(4)-反向传播
-
- 11.1 先睹为快
-
- 11.1.1 平衡杆游戏
- 11.1.2 Gym平台
- 11.1.3 策略网络
- 11.1.4 梯度更新
- 11.2 加强学习问题
-
- 11.2.1 马尔科夫决策过程
- 11.2.2 目标函数
- 11.3 战略梯度法
-
- 11.3.1 REINFORCE 算法
- 11.3.2 改进原战略梯度
- 11.3.3 带基准的REINFORCE算法
- 11.3.4 重要性采样
- 11.3.5 PPO算法
- 11.4 值函数方法
-
- 11.4.1 值函数
- 11.4.2 值函数估计
- 11.4.3 策略改进
- 11.4.4 SARSA算法
- 11.4.5 DQN算法
- 11.4.6 DQN变种
- 11.5 Actor-Critic方法
-
- 11.5.1 Advantage AC 算法
- 11.5.2 A3C 算法
加强学习是机器学习领域的另一个分支,除了监督学习和非监督学习。它主要利用智能身体与环境的互动来实现取得良好成绩的策略。与监督学习不同,强化学习没有明确的标记信息。只有来自环境反馈的奖励信息通常滞后。本章主要介绍DQN算法和PPO算法。
11.1 先睹为快
本节首先通过一个简单的例子来感受强化学习的魅力。本节以直观感受为主,无需掌握细节。
11.1.1 平衡杆游戏
如图所示,平衡杆游戏包括三个部分:杆、汽车和滑轨。汽车可以在滑轨上自由移动,杆的一侧通过轴承固定在汽车上。在初始状态下,汽车位于滑轨中央,杆垂直于汽车。智能车身通过移动汽车来控制杆的平衡。当杆与垂直方向的角度大于一定值或汽车偏离中间位置时,游戏结束。 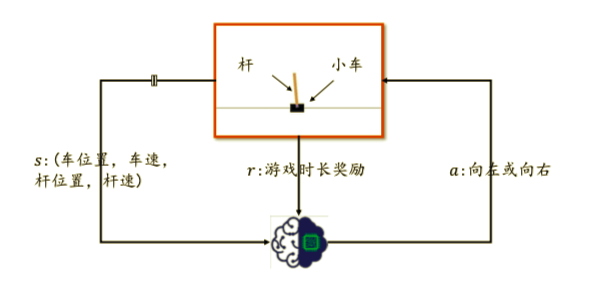 为了简化环境状态,我们直接将高层环境变量s作为智能主体的输入,包括汽车位置、汽车速度、杆角度、杆速度四个特点。智能体的输出动作a是向左或向右移动。将输出动作施加到平衡杆系统会产生新的状态,并获得奖励,可简单设置为1,表示时长加1。智能体通过环境状态每次戳t s t s_t st产生动作 a t a_t at,动作 a t a_t at在环境中产生新的环境状态 s t 1 s_{t 1} st+1,并获得奖励 r t r_t rt。
为了简化环境状态,我们直接将高层环境变量s作为智能主体的输入,包括汽车位置、汽车速度、杆角度、杆速度四个特点。智能体的输出动作a是向左或向右移动。将输出动作施加到平衡杆系统会产生新的状态,并获得奖励,可简单设置为1,表示时长加1。智能体通过环境状态每次戳t s t s_t st产生动作 a t a_t at,动作 a t a_t at在环境中产生新的环境状态 s t 1 s_{t 1} st+1,并获得奖励 r t r_t rt。
11.1.2 Gym平台
在强化学习中,可以直接通过机器人与真实环境进行交互,并通过传感器获得环境状态与奖励。但由于真实环境实验有一定复杂性和成本较高的问题,一般在虚拟环境上进行实验。 Gym平台是个虚拟的游戏环境平台,只需要通过少量python代码,就可以实现游戏环境的搭建与交互。
import gym
env = gym.make("CartPole-v1")
observation = env.reset()
for _ in range(1000):
env.render()
action = env.action_space.sample()
observation, reward, done, info = env.step(action)
if done:
observation = env.reset()
env.close()
11.1.3 策略网络
下边是强化学习中最为关键的环节,如何进行判断和决策。我们把判断和决策叫做策略(Policy)。策略的输入是状态s,输出是某个具体的动作a或着动作的分布 π θ ( a ∣ s ) \pi_{\theta} (a|s) πθ(a∣s),其中 θ \theta θ为策略函数 π \pi π的参数,可以用神经网络来参数化 π θ \pi_{\theta} πθ函数。 如下图,神经网络的输入是平衡杆系统的状态s,输出为所有动作的概率 π θ ( a ∣ s ) \pi_{\theta}(a|s) πθ(a∣s),即P(向左|s),P(向右|s)。并且: ∑ a ∈ A π θ ( a ∣ s ) = 1 \sum_{a \in A} \pi_{\theta}(a|s) = 1 a∈A∑πθ(a∣s)=1 其中A为所有动作的集合。 π θ \pi_{\theta} πθ网络代表了智能体的策略,称为策略网络。 策略网络的创建过程跟普通网络一样:
class Policy(tf.keras.Model):
def __init__(self):
super(Policy, self).__init__()
self.data = []
self.fc1 = tf.keras.layers.Dense(128, kernel_initializer='he_normal')
self.fc2 = tf.keras.layers.Dense(2, kernel_initializer='he_normal')
self.optimizer = tf.optimizers.Adam(learning_rate=0.001)
def call(self, inputs, training=None):
x = self.fc1(inputs)
x = tf.nn.relu(x)
x = self.fc2(x)
x = tf.nn.softmax(x, axis=1)
return x
def put_data(self, item):
self.data.append(item)
11.1.4 梯度更新
如果希望用梯度下降算法来优化网络参数,需要知道每个输入 s t s_t st的标注信息 a t a_t at,并且确保输入到损失值是连续可导的。强化学习和传统的有监督学习不同,主要体现在强化学习的标注并没有一个明确的好坏标准。奖励r可以一定程度上反应动作的好坏,但不能直接决定每个时间戳的动作。甚至有些游戏交互过程只有一个最终的代表游戏结果的奖励r,如围棋。那么给每个状态定义一个最优的动作 a t ∗ a^*_t at∗合理吗。首先游戏中的状态总数是非常巨大的,其次每个状态很难定义一个最优动作,有些动作虽然短期回报不高,但长期回报却是好的。
因此,策略网络的优化目标不应该是让每个输入 s t s_t st的输出尽量接近标注结果,而是要最大化总回报的期望。总回报是指从游戏开始到游戏结束之间的奖励和 ∑ r t \sum r_t ∑rt。
一个好的策略应该能让总回报的期望值最高 J ( π θ ) J(\pi_\theta) J(πθ)。根据梯度上升算法,参数更新如下: θ t + 1 = θ t + η ∂ J ( θ ) ∂ θ \theta_{t+1} = \theta_{t} + \eta \frac{\partial J(\theta)}{\partial \theta} θt+1=θt+η∂θ∂J(θ)
然而遗憾的是,总回报期望 J ( θ ) J({\theta}) J(θ)是环境给的,如果不知道游戏模型,是不可能通过自动微分求得 ∂ J ( θ ) ∂ θ \frac{\partial J({\theta})}{\partial \theta} ∂θ∂J(θ)的。
那么能不能在不知道 J ( θ ) J({\theta}) J(θ)的前提下,得到 ∂ J ( θ ) ∂ θ \frac{\partial J({\theta})}{\partial \theta} ∂θ∂J(θ)呢,其实是可以的,下面先给出表达式: ∂ J ( θ ) ∂ θ = E τ ∼ p θ ( τ ) [ ( ∑ t = 1 T ∂ ∂ θ l o g π θ ( a t ∣ s t ) ) R ( τ ) ] \frac{\partial J({\theta})}{\partial \theta} = \mathbb{E}_{\tau \sim p_{\theta}(\tau) } [(\sum_{t=1}^{T}\frac{\partial}{\partial \theta} log \pi_{\theta}(a_t|s_t))R(\tau)] ∂θ∂J(θ)=Eτ∼pθ(τ)[(t=1∑T∂θ∂logπθ(at∣st))R(τ)]
利用上边公式,只需要计算出 ∂ ∂ θ l o g π θ ( a t ∣ s t ) \frac{\partial}{\partial \theta} log \pi_{\theta}(a_t|s_t) ∂θ∂logπθ(at∣st),并乘以 R ( τ ) R(\tau) R(τ)就可以更新计算出 ∂ J ( θ ) ∂ θ \frac{\partial J({\theta})}{\partial \theta} ∂θ∂J(θ),按照 θ ∗ = θ − η ∂ L ∂ θ \theta^{*} = \theta - \eta \frac{\partial L}{\partial \theta} θ∗=θ−η∂θ∂L的方式更新策略网络,就可以最大化 J ( θ ) J(\theta) J(θ)。其中 R ( τ ) R(\tau) R(τ)为某次交互的总回报, τ \tau τ为交互轨迹 s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , . . . s t , a t , r t s_1,a_1,r_1,s_2,a_2,r_2,...s_t,a_t,r_t s1,a1,r1,s2,a2,r2,...st,at,rt。
11.2 强化学习问题
首先要了解一下强化学习的相关概念。具有感知和决策能力的对象叫做智能体(Agent),他可以是一段算法代码,可以是软硬件系统。智能体通过与外界环境进行交互完成某个动作。这里的环境(Environmont)是指接收到智能体的动作而产生影响,并给出相应反馈的外界环境的总和。对于智能体来说,他通过感知外界环境的状态(State),作出相应的动作(Action)。对于环境来说,它从某个初始状态 s 1 s_1 s1开始,通过接受智能体的动作而动态改变自身的状态,并给出相应的奖励(Reward)。
从概率角度描述强化学习过程,包括5个基本对象:
- 状态s 反应了环境的状态特征,在时间戳t上的状态记为 s t s_t st,他可以是原始的视觉图像,语音,文本等信息,也可以是高层抽象的特征,如小车速度,位置等数据。
- 动作a 智能体通过感知环境状态后作出的行为,在时间戳t上记作 a t a_t at。
- 策略 π ( a ∣ s ) \pi(a|s) π(a∣s) 代表了智能体的决策模型,接受输入状态s,给出决策后执行动作的概率分布 p ( a ∣ s ) p(a|s) p(a∣s),满足 ∑ a ∈ A π ( a ∣ s ) = 1 \sum_{a \in A}\pi(a|s) = 1 a∈A∑π(a∣s)=1 这种具有一定随机性的概率输出称为随机性策略。对应的为确定性策略。
- 奖励 r ( s , a ) r(s, a) r(s,a) 表示环境s在接受动作a之后,给出的反馈信号,一般是个标量,在一定程度上表明了动作的好坏。在时间戳t上的奖励记作 r t r_t rt,奖励一般具有滞后性。
- 状态转移概率 p ( s ′ ∣ s , a ) p(s^{'}|s, a) p(s