绝对光电编码器的基本结构和特点
由于外部干扰,增量光电编码器可能会出现计数错误,停电或故障停止后无故障
发现事故前执行部件的正确位置。绝对光电编码器可以避免上述缺点。绝对光电
编码器的基本原理和组件与增量光电编码器基本相同,光源、码盘、检测光栅、
由光电检测器件和转换电路组成。绝对光电编码器不同于增量光电编码器
数字是一种直接输出数字量的传感器,分别指示每个不同的增量位置。在它的圆形码盘上
上沿径向有几条同心码道,每条都由透光和不透光的扇形区域组成,相邻码道的扇形区域数量
是双倍关系,码盘上的码道数就是它的二进制数码的位数,在码盘的一侧是光源,另一侧对
每个码道应有一个光敏元件;当码盘处于不同位置时,每个光敏元件应根据光是否转换相应
电平信号,形成二进制数。这种编码器的特点是不计数器,可以在转轴的任何位置读取
与位置相对应的固定数字码。显然,码道越多,分辨率越高,对于一个有 N 位
二进制分辨率编码器,其码盘必须有N 条码道。绝对光电编码器原理如图1-8 所示。
绝对式光电编码器是利用自然二进制、循环二进制(格雷码)、二-十进制等方式进行光
电转换。绝对光电编码器和增量光电编码器的区别在于圆盘上的透光线和不透光线
根据读取码盘上的编码,绝对光电编码器可以有多个编码来检测绝对位置。其特点是:
角度坐标的绝对值可以直接读取;无累积误差;切断电源后不会丢失位置信息;编码器
精度取决于位数;最高运行速度高于增量光电编码器。
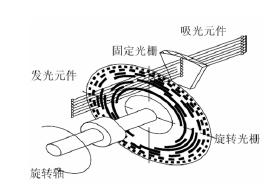
图1-8 绝对光电编码器原理
1.3.2 码制与码盘
绝对光电编码器的码盘可分为二进制码、循环码(格雷码)、
十进制码、六十进制码(度、分、秒进制)等。四位二元码盘(二进制、格雷码)如图所示
1-9 图中黑白分别表示透光区和不透光区。
图 1-9 四位二元码盘
图 1-9(a)是四位二进制码盘,其最里圈码道为第一码道,半圈透光半圈不透光,
对应最高位C一、最外圈为第n 码道,分为2n 亮暗间隔对应最低位置Cn,n 位二元
码盘最小分辨率为:
二进制马盘的缺点是每个码道的黑白分界线总有一半与相邻内圈码道的黑白分界线是
对齐,会因为黑白分界线描述不准确而造成粗误差。使用其他有权编码时也有类似之处
的问题。图1-10 是四位二进制码盘展开图,图中aa 黑白分界线是最高位码道的理想位置
它与其他三位码道的黑白分界线对齐。当码盘旋转并光束扫过该区域时,输出数
码从0111 变为1000 没有错误C1 道黑白分界线刻偏a’a当码盘转动时,输
数字将从01111出来 变为1111 再变为1000,中间出现了错误的数字111。C1 道黑白分界
线刻偏到a’’a当码盘旋转时,输出数字将从0111 变为0000 再变到1000,中间出现了
错误数字000。循环码盘(格雷码盘)可用于消除这种粗误差。
图 1-9(b)是四位循环码盘,与二进制码盘相同,码道数也等于数码位数,
因此最小分辨率也是式(1-2)求得,最内圈也是半圈透光半圈不透光,对应R1 位,最外圈
是第n 码道对于Rn 位置。与二进制码盘不同,第二码道也是半透光半不透光,第二码道是半透光半不透光i
码道分为2i-一个黑白间隔,第一个i 黑白分界线和码道的第一i-1 码道黑白分界线错开360° / 2i。
当循环码盘转移到相邻区域时,只有一个代码发生了变化。只要适当限制各码道的生产误差和安全性
安装误差,不会产生粗误差。由于这一原理,循环码盘得到了广泛的应用。
1.3.3 二进制码和循环码的转换
绝对光电编码器采用自然二进制或循环二进制(格雷码)进行光电转换
代码设计一般采用自然二进制码、循环二进制码、二进制码等。特点是不计数器
旋转轴的任何位置都可以读取与位置对应的固定数字码;抗干扰能力强,无累积误差;
根据不同的精度要求,电源切断后位置信息不会丢失,但分辨率由二进制位数决定,
可选择不同的分辨率即位数。目前有10个 位、11 位、12 位、13 位、14 等等。
绝对编码器采用循环二进制编码,其输出信号是一种数字排序,不是权重码,
不能直接比较大小和算术操作,也不能直接转换成其它信号,
通过一次代码变换,将其转换为自然二进制码,然后由上位机读取以实现相应的控制。代码变换
本文重点介绍了二进制格雷码与自然二进制码的交换。
(1)格雷码介绍(又称循环二进制码或反射二进制码)
只能在数字系统中识别 0 和1,各种数据只有转换为二进制代码才能处理。格雷代码是
典型的格雷码是一种具有反射特性和循环特性的单步自补码,
它的循环和单步特性消除了随机取数时出现重大误差的可能性。它的反射和自补特性使求反
非常方便。格雷代码属于可靠性编码,是一种错误的最小化编码方法,因为自然二进制码可以
但在某些情况下,比如从十进制的3 转换成4 时二进制
每个代码都必须改变,使数字电路产生大的尖峰电流脉冲。格雷代码没有这个缺点,它是
一种数字排序系统,其中的所有相邻整数在它们的数字表示中只有一个数字不同。它在任意
当两个相邻数之间转换时,只有一个数发生了变化。它大大降低了从一个状态到下一个状态
状时逻辑的混淆。此外,由于最大数和最小数之间只有一个数不同,通常称为葛莱反射码或
循环码。表1-1 几种自然二进制码与格雷码的对照表:
表 1-1 几种自然二进制码与格雷码的对照表
从表 1-1 可以得出十进制数的种类N 与n 二进制码满足以下关系:
可见二进制码是满足(1-4)关系的有权码,而格雷代码是无权码,不满足(1-4)
关系。它与相应的角度没有似(1-3),因此必须找出循环码和二进制码
对应关系和相互转换规则。
(2)二进制码转换为制格雷码
二进制码转换为制格雷码,其规则是保留二进制码的最高位作为格雷码的最高位,而二进制码作为格雷码的最高位,二进制码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷码作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格雷作为格作为格雷作为格作为格雷作为格作为格作为格作为格雷作为格雷作为格雷作为格雷作为格作为格雷作为格雷作为格雷作为格雷作为格作为格作为格作为格作为格作为格作雷作雷作为格雷作为格雷作为格雷作为格雷作为格作为格作为格作为格作为格雷作为格雷作为格作雷作为格作为格作为格雷作为格作为格
高格雷码是二进制码的高度与二进制码的高度不同,而格雷码的其余部分与二进制码的求法相似。
图1-11 将二进制码转换为格雷码。
图 1-11 自然二进制码转换为二进制雷码
图 1-12 将二进制码转换为格雷码的电路图(a)并行转换电路,图(b)
串行转换电路。使用串行电路时,工作前将进行D 触发器D1 置0,Q=0,在Ci 端送入
C1,异或门D2 输出R1=C1○ 0=C1,随后加CP 脉冲,使Q=C1;在Ci 端加入C2,D 输出R2=C2○
C1.以后可以依次重复上述过程。R1,R2,……,Rn。
(3)格雷码转换为二进制码
将格雷码转换为二进制码是保留格雷码的最高位作为二进制码的最高位,而二高位则是二进制码的最高位
高位二进制码与次高位格雷码不同,而其他二进制码与次高位二进制码不同
求法相似。图1-13 图为将格雷码转换为二进制码的电路(a)并行转换电路,图
(b)串行转换电路。使用串行电路时,工作前将进行JK 触发器D 置0,Q=0,将R1
同时加到J、K 端,再加入CP 脉冲后,Q=C1= R1。以后若Q 端为Ci-1 在J、K 端加入Ri。
根据JK如果J、K加入1CP脉冲后, i 1 Q C ? = ;若J、K 为“0”则
加入CP 脉冲后保持Q=Ci-1.这种逻辑关系可以写成:
图 1-13 格雷码转换为二进制码的电路
格雷码是无权码,格雷码盘获得的格雷码R1,R2,……,Rn 必须按图1-11 转换为
二进制码对应C1,C2,……,Cn 之后,可以替换(1-3)来确定相应的角度。
(4)实现格雷码与二进制码交换的软件方法
(a)二进制码转换为格雷码软件实现法
根据自然二进制转换成格雷码的规则,可以获得以下代码:
static unsigned int DecimaltoGray(unsigned int x)
{
return x^(x>>1);
}
实现了上述代码unsigned int 型数据到雷码的转换,最高可转换32 位自然二进
制码,超出32 位将溢出。
static int DecimaltoGray( int x)
{
return x^(x>>1);
}
//以上代码实现了 int 型数据到格雷码的转换,最高可转换31 位自然二进制码,超
出 31 位将溢出。
上述代码即可用于 VC 控制程序中,也可以用于单片机控制程序中。在单片机程序设计
时,若采用汇编语言编程,可以按相同的原理设计程序;若采用C 语言编程,则可以直接
利用上述代码,但建议用unsigned int 函数。
(b)软件实现法(参见示例工程中的 Gray to Binary )
根据二进制格雷码转换成自然二进制码的法则,可以得到以下的三种代码方式:
static unsigned int GraytoDecimal(unsigned int x)
{
unsigned int y = x;
while(x>>=1)
y ^= x;
return y;
}
static unsigned int GraytoDecimal(unsigned int x){
x^=x>>16;
x^=x>>8;
x^=x>>4;
x^=X>>2;
x^=x^1;
return x;
}
static unsigned int GraytoDecimal(unsigned int x)
{
int i;
for(i=0;(1<
{
x^=x>>(1<
}
return x;
}
//以上代码实现了unsigned int 型数据到自然二进制码的转换,最高可转换32 位格雷码,
超出32 位将溢出。将数据类型改为int 型即可实现31 位格雷码转换。
上述代码即可用于 VC 控制程序中,也可以用于单片机控制程序中。在单片机程序设计
时,若采用汇编语言编程,可以按相同的原理设计程序;若采用C 语言编程,则可以直接
利用上述代码,但建议用unsigned int 函数。
更详细请查看: http://bbs。elecfans。com/dispbbs_54_113406。html