从全新的角度提出改进方案 FM 方法，尝试在不同的实例场景中表示优化特征。

在实际应用中，在不同的数据实例中，相同的特征通常具有不同的预测能力，每个数据中最有用的特征也不同。 例如，在第一个例子中，特征 ??? 在以下情况下，点击概率显然至关重要：{年轻，女性，学生，粉红色，裙子 }。但在另一种情况下：{ 年轻，女性，学生，蓝色，笔记本 }，特征 ??? 重要性相对较低。

因此，需要在不同的数据实例场景中分配不同层次的预测能力，以更好地反映其具体贡献。

IFM估计公式为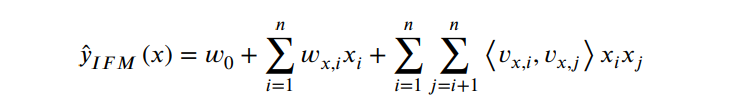： 第一项和第二项分别建模了数据的整体偏差和特征的阶权重，第三项捕获了准确的二阶特征交互。

在IFM 在方法中，公式中的第二项和第三项以非线性方式对不同数据条例的每个特征进行建模，可见权重 ??_x,?? 嵌入向量和每个特征 v_x,?? 不仅与第 ?? 个特征相关，而且与输入向量 x相关。

上图中深色部分代表FM新添加的零件除了原始模型。 以下是网络结构中每个具体环节的介绍

同FM一样，IFM也赋予每个特征相应的对应embedding对于上图中的x输入，由于x是离散变量转换为相应的one-hot因此，结果极其稀疏，我们在计算中只需要考虑1值的特征。假设每个样本总共具有h取值为1的特征，并将其对应的h取值为1embedding拼接，得到k * h维的向量Vx。

这部分是论文的核心创新点

它的主要功能是根据不同的样本计算样本的感知权重 m x , i m_{x,i} mx,i，并作用于一次性权重wi和embedding向量vi。子网络结构如下： 计算特征重要性的过程如下：

经过Factor Estimating Network得到输出mx,i，样本每个特征的一次权重和embedding向量进行refine，计算公式如下：

同FM一样，IFM结果如下：